 |
Vol IX No. 4 Winter |
|||||||||||||||||
 Submitted by Nancy Ricciardi of Clayton County School District.
Each school year seems to pass by more quickly than the previous year. I understand that is what happens as you get older. I think we attempt to accomplish more and more, and this keeps us busy throughout the year. At GCTM, we are continually planning for the next year's events before the current one ends.
GCTM will be hosting the annual Math Day at the Capitol on Tuesday, February 13, 2018. This is a great platform to emphasize the importance of mathematics education for the students in Georgia and to provide our mathematics teachers the opportunity to meet the legislators who debate and create educational policies for us. GCTM has also sponsored several visits to Georgia classrooms by legislators and we plan to continue this in 2018. Thank you, Advocacy committee and TJ Kaplan, for making this happen. We love to show off the great things happening in our schools!
The GCTM Executive Committee has a retreat scheduled for the beginning of 2018 to streamline our responsibilities, brainstorm ideas to better support Georgia math educators and to continue to improve communication between GCTM members. Be looking for updates on our website to stay informed about upcoming events. Please contact your GCTM Regional Representative or any member of the Executive Committee to offer your suggestions or questions as we continue to serve you and your interests as a mathematics teacher. GMC 2017 Photographs
To better plan your trip to the Capitol building, click here or see the information below:
Front Row (L to R): Senator Mike Dugan, Nikita Patterson, Joy
Darley, Bonnie Angel, Senator Chuck Hufstetler Additionally, GCTM appreciates the support of the Senator Matt Brass and Senator Tonya Anderson, who attended GMC this year. Both legislators were able to attend sessions and came away highly impressed with what they observed. Senator Anderson added that she "cannot wait to attend the conference again next year."
Teachers should emphasize important soft skills along with subject matter content; such soft skills will assist pupils to do well in acquiring mathematics content. Which soft skills might then be incorporated into teaching and learning strategies? Strategic Teaching of Soft Skills Objectives need careful scrutiny that pinpoints social and emotional learning known as soft skills. Soft skills might be imparted within the framework of learners achieving poignant knowledge and skills objectives of instruction. Teachers should be cognizant of the factors involved in teaching and learning, such as resilience and persistence. Too frequently, pupils give up on solving a word problem in mathematics out of frustration. Rather, the learner must be encouraged to pursue the solution(s) in spite of setbacks.
Maintenance, as a soft skill, is also poignant in that continuous effort must be put forth to achieve in oncoming learning opportunities. Frequently, a pupil might become hesitant in completing an assignment, and here is where maintenance of effort put forth is important. A very brief pep talk to motivate the learner might do the job in assisting a pupil to complete a task. Motivation is a salient skill for pupils to develop in wanting to grow and learn. Much time might be wasted when pupils stop to pause, for one or another, when continuous achievement is desired. Time wasted is time taken away from learning. This does not mean that pupils are like large containers whereby a liquid can be poured in continually. Learners do need time for stretching and exercising. Recess time is excellent for pupils to run, jump, skip, and do other of rigorous types of exercise. The body requires movement and motion for it to function well, mentally and physically in school and in society. Following wholesome exercise, the pupil is ready for cognitive activities in ongoing mathematics lessons and units of study. Learning Opportunities and Soft Skills in Mathematics The mathematics teacher must continue to stress soft skills within the framework of teaching and learning. Thus within each activity, the teacher of mathematics might emphasize empathy with the following:
The feeling dimension is involved in the concept of empathy; thus there are emotions inherent in empathizing with others. Social and emotional learnings are poignant in school and in society. There are a plethora of situations whereby individuals need encouragement and help to attain objectives of instruction, and here is where learners might well develop feelings of empathy. To languish by the roadside when an individual has been wounded should definitely be unthinkable. Rather aid must be provided to remedy the injury and take the wounded person to a hospital for treatment and care. So it is with more minor cases whereby needs must be met in time and place. Pupils in the classroom need assistance in mathematical problem-solving. Effort must be put forth by the learner, but there is a point of no return in feeling frustrated. Assistance must then be provided with bridging the gap. Feelings to help others and follow the Golden Rule is still very important.
Interest in mathematics is a key factor in teaching and learning situations. With pupils involved in learning due to interest factors, the chances for achievement improve. Mathematics teachers should select learning activities that capture the attention and interest of their students. Pupils who are turned off will not do well in ongoing activities. Teachers need to find ways for students to see the relevance of what they are learning. Pupils must perceive that each learning is vital and is worthwhile - not only in school but also in the societal arena. Mathematics then is perceived as possessing practical implications. Relevancy resonates throughout the curriculum. Students should be encouraged to see that we live in a mathematics world such as in
The utilitarian values of mathematics are endless. Mathematics, too, should be fascinating with its many enjoyable ongoing experiences in the curriculum! References Ediger, Marlow, and D. Bhaskara Rao (2014), Essays in Teaching Mathematics. New Delhi, India: Discovery Publishing House. Ediger, Marlow (2008), Modern School Mathematics, College Students Journal, 42 (2), 986-989. Resources on Soft Skills Teaching Soft Math Skills that Prepare Students for Any Career Teachers' hard and soft skills in innovative teaching of mathematics
Background:
Logarithms Before Calculus
Existed:
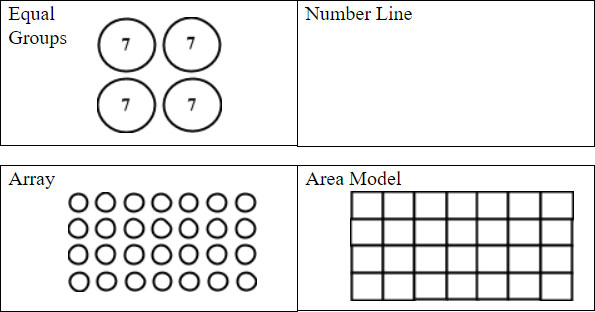
A classroom of fourth graders is presented with the following problem: Alex has 4 times as many marbles as Lucas. If Lucas has 7 marbles, how many marbles does Alex have? What might be happening as students try to make sense of the problem? Their background knowledge from third grade has helped them understand multiplication as equal groups of items and multiplication as the area of a rectangle. But how can they apply this understanding to the idea of 4 times as much? Will the tools and strategies they know, like equal groups, arrays, and area models, help them model this problem? Let's explore these issues as we consider interpreting multiplication as a comparison. After students have developed a robust understanding of multiplication as groups of and as area in third grade, they are ready to consider a new type of multiplicative relationship in fourth grade. The Georgia Mathematics Standards of Excellence introduce the concept of comparative multiplication through standard 4.MGSE.OA.1, which states: x 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5; and (b) Represent verbal statements of multiplicative comparisons as multiplication equations. (GA DOE, 2016, p. 32) Thus, students are comparing the multiplicative relationship between two sets of quantities in 4.MGSE.OA.1. Gojak and Miles (2015) describe it as thinking about one set of a "certain amount of items" as compared to "multiple copies of the first set" (p. 33). If we were to apply this interpretation to the opening problem, we could think of it as one set is the 7 marbles Lucas has as compared to Alex's four copies of those 7 marbles. We could represent the equation for that problem as 4 x 7 = 28; therefore, Alex has 28 marbles. In order for students to become proficient in interpreting comparative multiplication problems and modeling those situations as equations, they must first develop a conceptual understanding of this special multiplicative relationship. To support conceptual understanding, teachers should focus on two main instructional strategies: (1) present comparative multiplication problems in context; and (2) use hands-on and visual tools to represent the comparative relationship. As Lannin, Chval, and Jones (2013) note, "contextual situations provide a starting point for introducing and extending student understanding of multiplication" (p. 36). Context is powerful because students can visualize the situation, which will support them in making sense of the mathematics. Likewise, providing opportunities to physically model and draw visual representations of mathematics requires that students make sense of the relationships among quantities. It is important that this work takes place prior to introducing symbolic representations like equations, which are more abstract. In fact, "effective teaching of mathematics engages students in making connections among mathematical representations to deepen understanding of mathematics concepts" (NCTM, 2014, p. 24). Thus, teachers should support students in connecting how their interpretation of comparative multiplication situations is reflected in the physical models they build and/or the visual representations they draw, as well as connecting how those representations relate to the corresponding equation. Because comparative multiplication marks a departure from conceptualizing multiplication as groups of or as area (rows and columns or length and width), it is especially important to select appropriate tools in order to accurately represent the multiplicative relationship in comparative multiplication problems. In fact, "us[ing] appropriate tools strategically" is one of the Standards for Mathematical Practice (GA DOE, 2016, p. 6). Teachers must facilitate experiences to help students realize that particular tools or strategies may lend themselves well to represent certain mathematics concepts, just as they must realize some tools and strategies have limited usefulness. Specific to tools and strategies for multiplication, "each representation provides different insight into the multiplicative structure" (Lannin, et al., 2013, p. 40), which is certainly the case when introducing comparative multiplication. Based on the third-grade multiplication standards, fourth graders should have an understanding of multiplication as both equal groups and area. Thus, they have experience with physically and visually representing multiplication as groups of using tools such as building/drawing equal groups or jumping on a number line. They also have experience with representing multiplication as an area by building/drawing rectangular arrangements using arrays and area models. These tools, however, cannot accurately represent the comparative relationship in multiplication problems because there must be a visual representation of a comparison. In order to compare, each factor must be represented so that the difference (n times as many) is illuminated. That is the number of items and the copies of those items both must be represented in order to see the comparison. When representing multiplication with equal groups, the number line, arrays, and area models, only the groups of/rows and how many in each group/columns are represented as demonstrated in Figure 1.
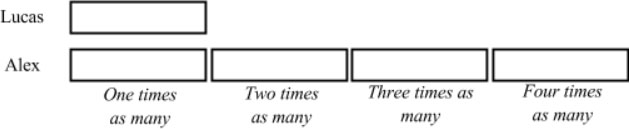
Figure 1. Multiplication strategies for 4 x 7 There is no representation of two sets of quantities in any of these models. Therefore, the tools used in the initial conceptualization of multiplication in third grade are not effective in representing the mathematics of comparative multiplication. As a result, fourth-grade teachers must look to other tools when introducing multiplicative comparisons. One of the best tools to illuminate the comparative relationship in a multiplicative comparison problem is the bar model, which is also known as a tape diagram (Common Core Standards Writing Team, 2011; Gojak & Miles, 2015; Van de Walle, et al., 2014). Bar models or tape diagrams capture the comparative relationships between the two sets of quantities as reflected in Figure 2. Alex has 4 times as many marbles as Lucas. If Lucas has 7 marbles, how many marbles does Alex have?
Figure 2. Initial model of opening problem Here we can see that Lucas has a certain amount and Alex has four copies of that same amount. We know the amounts are the same because equal-sized bars represent them. Also, notice how the four copies of the initial amount should be counted using the as many as language to reinforce the idea of copies (or multiples). To support students in using the bar model or tape diagram, it is recommended that they physically build the model first. Cuisenaire rods are an excellent manipulative for building bar models or tape diagrams because they do not represent a specific amount. Therefore, the emphasis can be placed on making sense of the situation and matching the comparison in a contextual situation with the model. Once students have physically modeled the multiplicative comparison, they can represent their model as a drawing and add more details as shown in Figure 3. Alex has 4 times as many marbles as Lucas. If Lucas has 7 marbles, how many marbles does Alex have?
Skip Counting: 7, 14, 21, 28; Alex has 28 marbles Equation: 4 x 7 = 28; Alex has 28 marbles Figure 3. Drawing of opening problem with details and possible solution strategies Once the bar model or tape diagram has been drawn and labeled, then students can use strategies such as skip counting or writing an equation to solve the problem. It is important that students refer back to the question to ensure that they only multiply the seven marbles four times, since the problem is asking about how many marbles Alex has, which is four times as many (or four copies of) the amount Lucas has. It is also important that the equation match the contextual situation, so the first factor should represent the as many times as (or copies of) amount and the second factor should represent the certain amount of items. In the case of the opening problem, the equation should be 4 x 7 = 28. As you can see, the bar model or tape diagram is a very effective tool for representing the comparison in comparative multiplication problems. Not only does it visually reflect the comparative relationship, it also supports students in making connections to more symbolic representations like equations. It is for these many reasons that fourth graders should use bar models or tape diagrams as the primary means for engaging in work with the 4.MGSE.OA.1 standard. Comparative multiplication is a new and challenging way for fourth-grade students to conceptualize multiplication. They must move beyond thinking about multiplication as groups of or as area (rows and columns) to consider the relationship between a set of a certain amount and a set of copies of that amount. Likewise, they must move beyond the multiplication tools and strategies they used in third grade to consider a more appropriate tool, specifically the bar model or tape diagram, to represent that comparison in comparative multiplication situations. When teachers help their fourth graders make connections among comparative multiplication situations, physical models and visual representations of bar models or tape diagrams, and equations, it is only then that the comparison is illuminated in comparative multiplication problems. References Common Core Standards Writing Team. (2011). Progressions for the common core state standards in mathematics: K, counting and cardinality; K-5, operations and algebraic thinking. Retrieved from https://commoncoretools.files.wordpress.com/2011/05/ccss_progression_cc_oa_k5_2011_05_302.pdfGeorgia Department of Education [GA DOE]. (2016). Georgia's standards of excellence: Mathematics: Kindergarten --fifth grade. Retrieved from https://www.georgiastandards.org/Georgia-Standards/Documents/Grade-K-5-Mathematics-Standards.pdfGojack, L. M. & Miles, R. H. (2015). The common core mathematics companion: The standards decoded, grades 3-5. Thousand Oaks, CA: Corwin Mathematics and National Council of Teachers of Mathematics [NCTM]. Lannin, J., Chval, K., & Jones, D. (2013). Putting essential understanding of multiplication and division into practice in grades 3-5. K. Chval & B. J. Dougherty (Eds.). Reston, VA: National Council of Teachers of Mathematics. National Council of Teachers of Mathematics [NCTM]. (2014). Principles to actions: Ensuring mathematical success for all. Reston, VA: Author. Van de Walle, J. A., Karp, K. S., Lovin, L. H., & Bay-Williams, J. M. (2014). Teaching student-centered mathematics: Developmentally appropriate instruction for grades 3-5 (2nd ed.). Boston, MA: Pearson. Dr. Andria Disney is an Assistant Professor of Elementary Mathematics Education in the College of Education at Georgia Southern University. Prior to receiving her Ed.D. from the University of Montana in 2016, she worked in public schools as an elementary teacher, a middle school math teacher, and a mathematics curriculum and instructional specialist. Dr. Disney's research interests include supporting pre-service and in-service teachers in making mathematics instructional change and using sense-making tools with their students. Back to Top
The banner for this issue was submitted by Nancy Ricciardi of Clayton County School District. What an interesting example of mathematics in the real world. An image like this could be used to jumpstart discussion of conversions, unit prices, or even other foods that are sold by the yard or foot. Nancy submitted this image after a request for banner submissions was posted to GCTM's facebook page. Have you found GCTM on facebook yet? Members post fascinating articles and topics and create mathematical discussion boards often as a way to connect to other mathematics teachers from all over the state to network. You should consider checking us out on Facebook.While you are at it, you should also consider contributing your own mathematical content to Reflections. Send in your ideas for banners, lessons, or mathematical research for publication to get your ideas out to our readers. Among the many benefits of being published in our journal, you will also have your annual membership waived for one year. A publication in Reflections is also a great TKES example of your professional knowledge via reading and contributing to mathematical journals.Do you see mathematics in the world around you? Are you taking chances in your classroom by trying more adventurous lesson plans? Have you tried new collaborative techniques that have lent themselves to increasing student achievement? We would love to hear your story. If so compelled, check out our publications page, send me an email of your submission. Don't forget to include a short bio and a picture of yourself! We at GCTM cannot wait to hear from you. The Spring Issue is right around the corner.
Membership Musings
Happy New Year! Welcome back for the second half of your academic year! What are your new year's resolutions for your teaching? For your students? For your professional life? Whatever they are, I am sure they include wishes for making all of these things better and more beneficial. Make someone else's professional life more beneficial by encouraging a colleague to join or renew membership in GCTM. We have so many benefits to offer them and you can be the catalyst to encourage their professional growth. Our membership stands at 1292 today. If everyone of you brought another member, we would be near 2500. Now go out there and do your teacher encourager thing! And make 2018 the best year ever ...for you AND for me!
The latest teaching trends and topics will include:
|
Table of Contents President's Message - by Bonnie Angel, GCTM President Advocacy Update - by Brian Lack, VP for Advocacy - by Dr. Marlow Ediger, Professor Emeritus, Truman State UniversityThe Logarithmic Chicken or the Exponential Egg: Which Comes First? - by Marshall Ransom, Senior Lecturer, Department of Mathematical Sciences, Georgia Southern University; Dr. Charles Garner, Mathematics Instructor, Department of Mathematics, Rockdale Magnet School; Laurel Holmes, 2017 Graduate of Rockdale Magnet School, Current Student at University of Alabama Illuminating the Comparison in Comparative Multiplication by Andria Disney, Ed.D. Georgia Southern University Editor's Note - by Becky Gammill, Editor GCTM Membership Report - by Susan Craig, Membership Director NCTM Report - by Michelle Mikes
|
|||||||||||||||||
|
Georgia Council of Teachers of Mathematics | PO Box 683905, Marietta, GA 30068 |
||||||||||||||||||
Plans
for the 2018 GCTM
Please
join us on Tuesday, February 13 at 9AM for the Fifth Annual Math Day
at the Capitol. For the second consecutive year, Senator Chuck
Hufstetler (District 52) will sponsor a resolution in support of a
high-quality mathematics education for all. GCTM members are invited
to sit in the Senate gallery and will be recognized after the
reading of the resolution. 
A high-quality mathematics
curriculum, taught by well-qualified teachers, must be offered to
all pupils. Learners need challenging experiences to be more
successful. With scaffolding, the mathematics teacher might motivate
pupils to attain more complex objectives of instruction. Vital
knowledge and skills objectives arranged sequentially may positively
influence students' attitudes toward mathematics.
As adults, individuals are
hesitant in facing dilemmas due to a lack of knowledge as to what is
inherent in solving personal and social problems. "Don't give up the
ship," might well be a useful slogan to follow in these situations.
In the school setting, the teacher needs to scaffold knowledge and
skills in guiding pupils in identifying and solving problems. In
mathematics problem solving, the pupil needs to analyze, synthesize,
and evaluate each involved sequential inherent step.
Then too, lost opportunities in
life accrue when individuals do not take advantage of what is good,
excellent, and has considerable merit, in decision-making
situations. Decision making from among hard choices is difficult
with its complexities. It takes motivation and time to pursue
selected alternatives. Thus in the mathematics curriculum,
problem-solving requires resilience in achieving solutions to
problem-solving experiences. Frustrations do occur. 
Mathematics teachers may struggle
to know when to step in when pupil frustrations occur and when is it
good to come to the aid of learner within an ongoing learning
opportunity. The answer, many times, might well be to bridge the
gap. This involves the pupil in being guided to find a solution to
the mathematical problem faced. Mathematics needs to be challenging
and invite engagement in activities and experiences.
Join thousands of your
mathematics education peers at the premier math education event
of the year! Network and exchange ideas, engage with innovation
in the field, and discover new learning practices that will
drive student success.