 |
Vol VII No. 4 Winter 2016 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Welcome to the winter edition of Reflections, the Georgia Council of Teachers of Mathematics quarterly publication. So much has transpired since the last edition of Reflections was released! The final results of the 2014 Winter and 2015 Spring Georgia Milestone Assessments were released in October, providing a wealth of much-anticipated data through which to sift and decipher. Some of you who teach high school have already given the 2015 Winter Milestone in December. Hopefully, these assessment results will provide opportunities for conversations centered on authentic ways to affect student achievement. I would recommend Visible Learning for Teachers: Maximizing Impact on Learning by John Hattie as a book that can frame these discussions for highly effective strategies for the facilitation of learning as well as NCTM's Principles to Actions. The Georgia Mathematics Conference 2015 was a jam-packed event on October 14th, 15th, and 16th. The theme of this year's conference, Growing Student Potential in Mathematics, was evident in the presentations, workshops, and sessions provided by keynote, featured, and volunteer speakers. The theme allowed us to focus on two major areas of research: motivating our students to grow their minds and classroom implementation of the eight Effective Mathematics Teaching Practices as outlined in the NCTM publication Principles to Action. Each conference participant received a copy of Principles to Actions, enabling each one to open to exact passages as various speakers made references. We also held our very first "conference-within-a-conference" for leadership on Thursday afternoon, targeting state, district, and school-level leaders to make all stakeholders aware of the latest findings on how people learn and of the challenges facing mathematics teachers in today's classrooms. The beautiful weather served as a backdrop as GCTM members were provided with opportunities to grapple with new mathematical concepts and explore resources to incorporate into their own teaching practices. With another successful GMC completed (see the GMC collage below), GCTM looks forward to new events on the horizon, such as Math Day at the Capitol 2016 on February 8th and the NCTM Summer Academies on July 11-16, 2016. More information on these events will be forthcoming As we move into the New Year, we also welcome our newly elected GCTM officers: Michelle Mikes as Secretary and Joy Darley as Vice-President for Constitution and Policy. Michelle is the Mathematics Supervisor for the Division of Instruction and Innovation Practice for Cobb County Schools, and Joy is an associate professor in the Department of Mathematical Sciences at Georgia Southern University. We are excited about the leadership that these new officers will bring to the GCTM Executive Committee. Sometimes the winter months can seem dark and gloomy and long. Keep fighting the good fight with your eyes on the prize of fostering student learning! The warmer days of Spring are right around the corner.
Mini-Grants are awarded in any amount up to $300 and are awarded on the criteria that the proposals highlight creative innovations, provide potential to impact student learning or for replication by and dissemination to other teachers, and advance NCTM's Principals and Standard for School Mathematics. This year's mini-grant recipients include:
For more information about Mini-Grants or Funds for Special Projects, please visit GCTM's Grants page. Other award recipients were also recognized for their expertise, passion, and leadership in teaching mathematics at this year’s Georgia Mathematics Conference at Rock Eagle. Congratulations to the following awardees.
Speakers at this event included Dr. Gilda Lyon, from the Georgia Department of Education STEM Office, Georgia Senator John Wilkinson (pictured to the right), and Matthew Gambill, President of the Georgia Association for Career & Technical Education. Each speaker provided insights and updates into the current state of STEM education in Georgia as well as ways to advocate for the teachers and students here in our state. Kaycie Maddox, President, Denise Huddlestun, Vice-President for Advocacy, and Chuck Garner, Vice-President for Competitions, represented GCTM at the STEM Leadership Forum.
GCTM President-Elect Bonnie Angel, GCTM V.P of Advocacy Denise Huddlestun and GCTM Secretary Debbie Kohler attended the 2015 NCTM Affiliate Leadership Institute in Phoenix, AZ July 14 – 16. Three main focuses for the conference included networking with other affiliate leaders across the United States, continuing to work on the strategic plan for GCTM, and studying change with discussions from Switch: How to Change Things When Change is Hard (Chip & Dan Heath). This book involved looking at problems in schools and classrooms with a desire to change. There are three main ideas involved with “Switch” – the Rider, the Elephant and the Path. Each of these ideas was developed in a method that the leaders involved learned ways to effect change. The Rider is our rational side. It is important to direct the rider by following the bright spots in the classroom, script the critical moves and point to the destination. Directing the rider might include studying what has worked in the past, or looking for bright spots in the classroom. One might also look at other situations that are similar but had positive outcomes. For a difficult student, this could mean greeting them in a positive way as they come in the door or giving them problems to solve that they had access to. Scripting critical moves means that one has to be specific instead of looking at the big picture. In order to “switch” and create change, the behavior must be scripted and done so in a way that eliminates ambiguity. Laddering down to a specific behavioral goal is also a possibility. Finally, the rider needs to have a destination. It is critical to point to that destination as well as ensure that it is a rich destination – one that is important.
The Elephant is the second part of the “Switch” process. The elephant represents our emotional and instinctive side. Its strengths are love, compassion, sympathy and loyalty. To make progress toward a goal requires the energy and drive of an elephant, but the elephant must also be motivated. Motivating factors include using pictures or graphs to track progress. Breaking down the change until it no longer spooks the elephant is helpful. Also, limit the investment you are asking for and set small goals. The elephant must be kept moving forward, given motivation and helped to feel confident and needed. Cultivating a sense of identity and instilling a growth mindset allow the elephant to move forward and shrink the change. The Path is the final component of the “Switch” mindset. Shaping the path includes tweaking the environment and building a habit. Tweaking the environment means recognizing that what looks like a person problem may be a situation problem. When the situation changes, the behavior will change. If the right behaviors are made a little easier and the wrong behaviors are made harder, then the path is changed. When the path is changed, the behavior changes also. Building a habit that involves autopilot opportunities with action triggers can create an ‘instant’ habit. Action triggers are better than harder goals. Leaders who instill them reinforce their team’s goals and make “free progress.” A good change leader thinks “How can I set up a situation that brings out the good in these people?” Good habits should advance the mission and be easy to embrace. Thus, the “Switch” mentality involves three main ideas --- 1) Speak to the Riders by pointing to the destination, 2) Appeal to the identity of the group (elephant) and 3) Rally the herd by establishing a group norm. Affiliates from each state also worked on the Strategic Plan for their state. Since Georgia has a strategic plan, action steps were developed for the strategic plan for three specific goals. The Georgia leaders worked on strategic steps for promoting a high quality mathematics education for all students, promoting ongoing professional development for mathematics education and for effective internal organization and execution in order to meet objectives. Breakout sessions allowed for Georgia representatives to meet with representatives from other states and learn what each state was doing for Mathematics Education. Grant availability, future NCTM Annual meeting dates, and best practices in mathematics were also discussed. Leaders also met with Diane Briars, President of NCTM, to discuss what NCTM is doing and how it operates. Georgia’s goals and standards are very close to the goals and standards of NCTM, so many of the other states’ leaders wanted Georgia to share information. We presented information about the Georgia Summer Academies, and individually spoke with other groups about many things that Georgia’s GCTM does well including our conference, advocacy and the use of our website. The Georgia leaders left with more knowledge as well as positive goals to help improve and sustain the state organization.
Georgia Education Leadership Institute
Advocacy With the assistance of Tyler Kaplan, the legislative consultant assisting GCTM in advocacy efforts, GCTM representatives met with a leader from both the House and the Senate to promote the importance of a quality mathematics education in Georgia. Kaycie Maddox and Denise Huddlestun met with Senator Lindsey Tippins, Senate Education Chairman, and Representative Brooks Coleman, Chairman of the House Education Committee, to make them aware of GCTM’s mission and purpose. The Education Reform Commission expressed their appreciation for our discussion of the adoption of 1)a regular curricula adoption cycle and 2) the importance of professional learning for teachers. As the President of GCTM, Kaycie made a public comment at the end of the Education Reform Commission meeting on October 22, 2015 to communicate our support of these two items being considered by the Commission. Find out more information about the Education Reform Commission.
The third annual Math Day at the Capitol is tentatively scheduled for Monday, February 8, 2016 pending confirmation of the legislative calendar. Representative Mike Dudgeon will sponsor a resolution to be read in the House that day. When the resolution is read, representatives from GCTM will be recognized on the floor of the House and other GCTM members in the gallery will be recognized. Rather than sponsoring a breakfast with limited time to engage in conversations with legislators about the importance of a quality mathematics education program in the state, a lunch and learn is tentatively scheduled for key leaders in the education committees of both the House and the Senate. A few GCTM representatives will present information and offer an opportunity for discussion while providing the lunch.
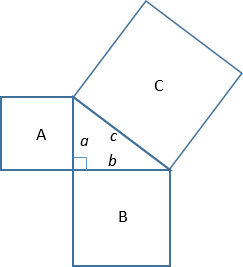
As I reflect over the last 24 years in math education, I realize how much better I have become as a teacher. I think back to those first few years teaching middle school. Yours is not to reason why, just invert and multiply was how I taught division of fractions! I am embarrassed to admit that I resorted to short cuts and silly songs but I was doing the best I knew to do at the time. Students would ask me why a certain procedure was used, and I didn’t always know the answer. I was troubled when students would mix up procedures or apply mnemonics to incorrect situations. I knew that I needed to do something different. I was teaching at a very superficial layer. My journey into improving my teaching happened very early in my career and continues to this day. I had to teach myself conceptual understanding to accompany the procedural skills that I already had. I quickly learned the power of having students use manipulatives to discover mathematics. Manipulatives provide a kinesthetic way to represent what could be very abstract concepts to students. I began slowly by using two-color counters to teach addition and subtraction of integers, algebra tiles to model solving equations, and Cuisenaire rods to teach ratios and fractions. Students can see, feel, move, and talk about mathematics by using manipulatives. Their eyes light up when the mathematics was revealed through the use of manipulatives. Finally, concepts were beginning to make sense to students! It hasn’t always been easy. Sometimes the manipulatives backfire. If the problems are not carefully planned out, the manipulatives may not reveal the mathematics, or they may be too troublesome to use. I still struggle with using manipulatives to demonstrate division of integers. I refuse to use geoboards in my middle school classroom because arming middle school students with rubber bands scares me. However, I continue to seek out new ways to help students discover concepts with manipulatives. This year, I planned a series of lessons to introduce the Pythagorean Theorem to students. I wanted students to have a solid grasp of the relationships of the sides in a right triangle before introducing them to the formula. This lesson addressed the standard, MGSE8.G.6, where students are to be able to explain a proof of the Pythagorean Theorem and its converse. There are multiple resources available for students to discover this relationship. The state teacher edition (https://www.georgiastandards.org/Georgia-Standards/Pages/Math-6-8.aspx) contains a Spotlight Task, The Pythagorean Relationship, which leads students through a discovery activity. Students draw a right triangle on grid paper, form squares on each side, find the areas of the squares and look for the relationship. In my class, we performed more of a hands-on approach by cutting out the two smaller squares and reassembling them to fit on top of the square formed on the hypotenuse. In particular, I used an activity from AIMS Education Foundation, A Pythagorean Puzzle, from Looking at Geometry. The physical movement of the pieces reinforced the concept of area and the relationships between the areas on each side. As we progressed through then unit, I frequently heard students distinguish between areas and side lengths as they discussed problems and helped each other. “You forgot to find the area – you were just using the side length.” We spent one class day discovering the relationship. I closed the lesson by reviewing the relationship using the model. At this point, I still had not formally introduced the Pythagorean Theorem.
I asked questions such as:
Students were able to successfully answer each of the questions and truly had a good grasp of the concept. On the second day, we discovered the converse of the Pythagorean Theorem using the Triangle Discovery activity. Students cut out squares from grid paper and used them to create triangles. Using the manipulatives, students discovered how to determine if a triangle was an acute, right, or obtuse triangle given the side lengths. This activity connected nicely to a previously learned concept from seventh grade (MGSE7.G.2) where students are to “explore various geometric shapes with given conditions. Focus on creating triangles from three measures of angles and/or sides, noticing when the conditions determine a unique triangle, more than one triangle, or no triangle.” Students remembered that the sums of any two sides of a triangle must be greater than the third side in order for a triangle to be formed. This activity allowed them to delve further into the concept to determine the type of triangle formed based on the side lengths. Students referred to the grid paper manipulatives as they made generalizations. I heard comments such as, “When c2 is larger than the a2 and b2, the a2 and b2 squares have to stretch out to make the triangle. That is why an obtuse triangle is formed.” I recommend using fairly large grids such as centimeter grid paper or larger. For some of the triangles, if they are not carefully lined up, could appear to be a right triangle. If this happens, address it during the lesson debrief and reach class consensus on the type of triangle.
I debriefed the lesson using questions such as:
Up until this point, I still had not officially introduced the theorem to the students in its traditional form, a2 + b2 = c2. Students were able to successfully answer all of the questions based on the experience they had with the manipulatives. On day three of this mini-unit, I introduced the traditional form of the Pythagorean Theorem to students. Because of the activities we had completed, expressions such as a2, b2, and c2 had meaning to them. As we continued through the unit, they constantly referenced these introductory activities. The initial two days I spent with discovery activities at the beginning of the unit not only were engaging and meaningful to students, but they “bought” me extra time as we progressed through problems and applications. I did not have to spend additional time reteaching the theorem, the relationships, or vocabulary. The conceptual development had laid a firm foundation for procedural fluency. Resources: Looking at Geometry. (2009). AIMS Education Foundation, Fresno, CA. Dina Sherwood teaches math at Barber Middle School in Cobb County. Prior to Barber, Dina served as Cobb County's secondary math coach for their Title I schools. Dina's career began in Texas where she taught middle school and high school math, served as a district math coach, and was the senior math consultant for Region 4 Education Service Center.
Interactive Notebooks were a hot topic this summer at the GCTM Summer Math Academies. During the summer sessions, teachers who teach kindergarten through 2nd grade students learned how to support classroom tasks and learning activities through various independent notebook ideas. Initially, participants set up a notebook and added several activities to it as they participated in tasks throughout the two-day academy. It is important to note that Interactive Notebooks are a tool to support instruction; they do not replace instruction or tasks in the classroom. Students desire creativity and a way to express their ideas, and teaching students how to create notebooks encourages this process. The activities highlighted in the summer academies illustrated how to accomplish this in kindergarten through second grade settings. Session activities embedded writing opportunities for participants that demonstrate how students can process the information they had learned from a given task. All of the activities shared during the two days showed how students can use their notebooks to review and practice skills and concepts over and over again. When setting up interactive notebooks in your classroom, consider getting parent volunteers to help out. This will save class time, keep the notebooks uniform, and include parents in the students’ learning. A volunteer could number the pages, glue in the beginning organizers, and even help label the notebooks with student names for kindergarteners. However, students should still be encouraged to decorate the front cover of the notebook. Doing so helps students understand that the notebook is theirs and will give them ownership over the care of the notebook. A special thanks to Jennifer Smith for sharing her resources and ideas with GCTM Academy organizers. Jennifer allowed the academy participants to use her ideas and several of her Interactive Notebook tasks for free. Summer academy participants learned a few tips and techniques for setting up their notebooks to support the frenzied pace of a primary classroom. On the inside front cover of the notebooks, they glued 6 x 9 inch manila envelopes and labeled them “My Safe Place.” This envelope can be a student and teacher lifesaver during those times in class when a student did not get completely finish with a task but has some of the pieces that need a safe place to stay until they complete the task. For example, when a student has several pieces left to glue into place, but it is time to leave for lunch, the remaining pieces can be placed in the envelope until the student has time to finish the activity. This idea was a favorite of the academy participants and was used several times throughout the two-days to keep small pieces or work that needed to be finished later.
As all K-2nd grade students are required to learn about informational text, the Interactive Notebook is a great place to make setting up a booklet a real-life learning experience. The numbered pages of the notebook help K-2nd graders apply the idea of a book’s not skipping pages and moving in the direction of left to right. The very first page of our summer notebooks was numbered as page 1 and became our “Title Page.” On the title page, participants wrote their first and last names, as well as their instructors’ names, just as students do in the regular classroom.
The second page of the notebook became a place to add a rubric for scoring activities, and page three was saved for gluing the rules for the proper care and use of the notebook in the classroom. It is important to remember that establishing rituals and routines for the use of the notebook with the students is an important classroom management requirement. It is better to set the learning stage in the beginning so that students know what is expected at all times. For more specific instructions on setting up an Interactive Notebook, please see the video below. Once the notebook skeleton has been created, I provide copies of the rubric and a copy of the rules to my students. (See the resources below.) After setting up the notebooks, the academy participants began to add different activities that mimicked the tasks done in class. An academy favorite was the number line activity. Participants wrote addition and subtraction problems to represent the different common addition and subtraction situations. The different problem types are helpful in building an in-depth understanding of these operations, and it is important to include all the types of these problems in the math classroom. The written math problems were then used to act out the problems on a huge number line which really made the participants think about the unknown part of the problem. Participants used hats with symbols such as a square to represent the “start,” a triangle to represent the “result,” and a frog to represent the “change,” while acting out the word problem on the number line.
These same representations were then recorded in the Interactive Notebook. The idea is for the students to experience the interactive number line as an activity in math class and to transfer the information into the notebook as an independent review.
Interactive Notebooks can be a great tool to support instruction in the primary classroom, but there should be a strong connection between the math class and the interactive activity so that students develop an in-depth understanding of the big ideas for a strong mathematical foundation. Are you interested in implementing Interactive Notebooks into your instruction? I’ve included some links below to help you get started. Interactive Notebook Resources: Setting up an Interactive Notebook Kindergarten Number Line Activity Second Grade Number Line Activity Interactive Notebooks for Secondary Classrooms Kristi has 19 years of teaching experience, and has taught Kindergarten, 2nd grade and 5th grade as a homeroom teacher. For the last 6 years, she worked as an Academic Coach helping teachers from Pre-K through 5th grade in all academic subjects, but her favorite is mathematics. She holds a Specialist degree in Leadership and Administration as well as a certificate as a Teacher Support Specialist.
Students really enjoy this a differentiated 8th grade State Performance Task which could easily adapted for other grade levels. Through the activity, students discover whether there is a relationship between the weight of cotton lint and the number of seeds that it contains, and students also develop possible related equations that they could give to a farmer to predict their profit. To begin this task, I put in front of the students samples of cotton products and have them brainstorm what all of them have in common. Next, they get to pick their own cotton boll from a cotton plant. Students get to take a virtual tour with a cotton farmer to see the harvesting of cotton and ask their questions through face time. I was able to set this up with a neighbor that knew a cotton farmer. If you don’t have access to a farmer, I would suggest contacting your local county extension office to make a contact. Then, they get to experience picking the cotton lint out of the boll followed by picking the seeds out of the cotton lint [This is the part that the GMC participants discussed about the presentation].
Students realize that it takes about 10 minutes to pick the seeds from the lint, and we discuss what this would be like to do for 8-10 hours every day. This leads to the discussion on the pros and cons of industrialization. While they are picking the seeds, they listen to the history, economics and science of cotton farming through a video created by The University of Tennessee AG Research.
To wrap up the activity, we celebrate by snacking on cotton products such as Chips Ahoy, Ritz Crackers and Mary Janes, and the students take a museum walk with the artifacts of the Cotton Kit provided by the Georgia Cotton Commission while they are snacking. The Cotton Kit contains lesson plans and three brief articles. I gave these to the Georgia History teacher to use in her class where students collaborated and summarized each article in groups. They presented their findings back in my math class the next day. I asked the class math related questions to their findings during each presentation. Then, I revealed who had the most accurate line of best fit based upon the linear regression found on the TI84. The task took two math/history class periods of 50 minutes each.
The cotton kit contains lesson plans with information on the history and economics of cotton, as well as sample artifacts. The materials needed for this task include cotton bolls, measuring devices, stop watch/smart phone, and a cotton kit. Additionally, students will need computer access for video/statistics, cotton snack products, and baggies so that students can take their organic cotton home with them.
Additional Resources:
Images to use with this activity or with your students:
Michelle has over 20 years of teaching in middle and high school mathematics. She was recipient of the John Neff Award in in 2012. She is currently the Mathematics Supervisor for the Division of Instruction and Innovation Practice for Cobb County Schools.
We are excited to offer this new feature of Reflections. Email all inquiries to the Reflections editor, Becky Gammill. Winter’s Featured Artwork: Archimedes
Abraham Diakite, Kennesaw Mountain High School, Marietta, Georgia
Membership is at an all time low! Can you help us answer these questions?
GCTM has a long and effective history for helping shape and support the teachers and students of Georgia, with the most effective mathematics instruction. It needs YOU and your colleagues to exist and thrive. GCTM has had such a significant effect on my classroom for decades. I hope that once you reflect on the positive outcomes you have seen from GCTM events and membership, you will press that RENEW button on the website and be an active member! GCTM needs you!
This issue of Reflections comes filled with lessons that focus on student activities which are both hands-on and engaging. The three articles respectively presented by Kristi Caissie, Dina Sherwood, and Michelle Mikes offer tasks and strategies that can be useful at all grade levels. Kristi discusses Interactive Notebooks and how they were used during the 2015 Summer Academies. Dina suggests a hands-on method for presenting the Pythagorean Theorem in a conceptual way, and Michelle explains the novel adaptation of the Cotton Boll task that she presented at this year’s GMC. So whether you want to try an interdisciplinary task, learn strategies for helping students discover and record their notes interactively, or extend your knowledge about old topics in new and interesting ways, these articles undoubtedly have something for you! And don’t pass up our new Reflections contributor incentive! Each of the three authors above will have her annual GCTM membership renewed at no cost as a reward for contributing. Do you have something to share that might benefit others? Don’t hesitate to email me your lessons, articles, and reflections for possible publication in this journal and have your membership renewed for free. I’m happy to report that your Georgia Council of Teachers of Mathematics has done a great job of representing Georgia math teachers by attending numerous state and national conferences this Fall. Please check out our updates of GCTM’s involvement at the 2015 NCTM Affiliate Leadership Conference, the 2015 Georgia STEM Leadership Forum, the Georgia Education Leadership Institute, and our communication with the Education Reform Commission. We also have another Math Day at the Capital scheduled for this coming spring which will allow GCTM even more opportunities to interact with state legislators while positively advocating for mathematics teachers in Georgia. Finally, a few additional math circle resources have come to our attention since we went to press with the Fall issue of Reflections. As you may know, math circles are an interesting way to get students to discuss mathematics and solve problems for recreational purposes. Chuck Garner, GCTM’s Vice President for Competitions, has provided some great additional resources for creating math circles within different settings. He suggests that the best math circle books are found at the American Mathematical Society Bookstore website. However, he also notes that “this series published by the American Mathematical Society is great, but the ones I strongly recommend are the first two volumes, A Decade of the Berkley Math Circle, and Math Circle in a Box. Additional references Chuck points to are the math-circle-specific Special Interest Group of the Mathematical Association of America, the National Association of Math Circles, and the Math Teachers’ Circle Network. Of course, our favorite math circle is the one that includes you, and from all of us here at Reflections, we wish a happy, safe, and most of all relaxing holiday break to all our wonderful GCTM family. We look forward to lots of good things in 2016 and we’re excited you’re with us!
Founded in 1920, the National Council of Teachers of Mathematics (NCTM) is the world’s largest mathematics education organization, with 80,000 members and more than 230 Affiliates throughout the United States and Canada. Interested in Membership? Learn more about exclusive member benefits and discounts and join today at NCTM.org, Membership. NCTM A
|
Table of Contents President's Message - by Kaycie Maddox Congratulations to this GCTM's 2015 Award Recipients! 2015 Georgia STEM Leadership Forum Update - by Kaycie Maddox 2015 NCTM Affiliate Leadership Conference - by Debbie Kohler GCTM Secretary 2013 - 2015 GCTM Advocacy Report - by Denise Huddlestun Vice President for Advocacy Conceptual Development of the Pythagorean Theorem - by Dina Sherwood Integrating Interactive Notebooks into a Task-Centered Classroom - by Kristi Caissie What Does Cotton Have To Do With It? Otherwise known at The Cotton Boll - by Michelle Mikes Calling All GCTM Members…Present and Past! - by Susan Craig, Membership Director Notes from the Editor - by Becky Gammill, Ed.D., Publications Editor NCTM News! - by Dottie Whitlow
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Georgia Council of Teachers of Mathematics | PO Box 5865, Augusta, GA 30916 | 1-855-ASK-GCTM |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
























 The
purpose of the forum was outlined as: “Bringing excellent STEM
education to all students requires STEM leaders who not only
understand good teaching but also have the ability to advocate for
students at local and state levels. This special workshop provided
an excellent lead-in to the Georgia STEM Forum by giving STEM
leaders the tools they need to promote STEM education across the
state.”
The
purpose of the forum was outlined as: “Bringing excellent STEM
education to all students requires STEM leaders who not only
understand good teaching but also have the ability to advocate for
students at local and state levels. This special workshop provided
an excellent lead-in to the Georgia STEM Forum by giving STEM
leaders the tools they need to promote STEM education across the
state.”


 In
an effort to raise awareness of GCTM and its mission, GCTM had a
table at the 2015 Georgia Education Leadership Institute: Supporting
Student Success!The annual event, sponsored by the Georgia
Department of Education and the National Center for Youth Issues,
provides an opportunity to bring together leaders from many fields
interested in promoting and improving education in Georgia and was
held at the Marriott Marquis in Atlanta September 9 - 11. GCTM
representatives had access to speak to district, state, and building
leaders to inform them of GCTM’s mission and purpose and to extend
an invitation to attend the Leadership Strand of the Georgia
Mathematics Conference. Dottie Whitlow, NCTM Representative, spoke
with Superintendent Richard Woods during one of the breaks at the
conference. (See photograph below.) Other GCTM Executive Committee
members who helped with the table were Kaycie Maddox, GCTM
President; Bonnie Angel, GCTM President Elect; and Denise Huddlestun,
VP for Advocacy.
In
an effort to raise awareness of GCTM and its mission, GCTM had a
table at the 2015 Georgia Education Leadership Institute: Supporting
Student Success!The annual event, sponsored by the Georgia
Department of Education and the National Center for Youth Issues,
provides an opportunity to bring together leaders from many fields
interested in promoting and improving education in Georgia and was
held at the Marriott Marquis in Atlanta September 9 - 11. GCTM
representatives had access to speak to district, state, and building
leaders to inform them of GCTM’s mission and purpose and to extend
an invitation to attend the Leadership Strand of the Georgia
Mathematics Conference. Dottie Whitlow, NCTM Representative, spoke
with Superintendent Richard Woods during one of the breaks at the
conference. (See photograph below.) Other GCTM Executive Committee
members who helped with the table were Kaycie Maddox, GCTM
President; Bonnie Angel, GCTM President Elect; and Denise Huddlestun,
VP for Advocacy.
 Math Day at the Capitol
Math Day at the Capitol









 Pringles, car tires, cosmetics, ice cream, Levi
jeans, explosives and Laffy Taffy. What do all of these things have
in common? Cotton! Cotton is Georgia’s only food and fiber crop, as
well as the leading crop in the state. The United States has the
purest and most desired cotton in the world. What does this have to
do with math? The list is long, but there are ways to engage
students in applicable, relevant mathematical activities, and one
such way is with the Cotton Boll task developed by Carrie Pierce of
Lee County Schools.
Pringles, car tires, cosmetics, ice cream, Levi
jeans, explosives and Laffy Taffy. What do all of these things have
in common? Cotton! Cotton is Georgia’s only food and fiber crop, as
well as the leading crop in the state. The United States has the
purest and most desired cotton in the world. What does this have to
do with math? The list is long, but there are ways to engage
students in applicable, relevant mathematical activities, and one
such way is with the Cotton Boll task developed by Carrie Pierce of
Lee County Schools.
 If
you are interested in implementing this task in your classroom, keep
in mind that Georgia typically harvests cotton in October/November.
So, check with your local extension agent to connect with a cotton
farmer and the Georgia Cotton Commission (see link below) to obtain
a “cotton kit.”
If
you are interested in implementing this task in your classroom, keep
in mind that Georgia typically harvests cotton in October/November.
So, check with your local extension agent to connect with a cotton
farmer and the Georgia Cotton Commission (see link below) to obtain
a “cotton kit.”  This
is a great integrated, interesting task for students that actively
engages them. Performance tasks may be brought to life with a few
materials, videos and collaborative settings. This activity
incorporates 3-Act Tasks by using cotton related videos online,
STEM/Interdisciplinary lessons which are found in the cotton kit,
and Problem Based Learning through discussions of the eradication of
the Boll Weevil and issues of cotton farmers today that need
resolving-which could extend this task. It is through the
intersection of these three instructional tools – 3-Act Tasks,
STEM/Interdisciplinary lessons, and PBL - where students create
memorable, relevant experiences from real world scenarios that
students would not typically have access to. This is authentic
learning. Take a given task and bring it to life by creating a
hands-on experience for students. This will most likely require some
revision, and is enhanced with a real life problems or situations
for students to find possible solutions. Your students will thank
you for it. Keep Calm and Cotton On!
This
is a great integrated, interesting task for students that actively
engages them. Performance tasks may be brought to life with a few
materials, videos and collaborative settings. This activity
incorporates 3-Act Tasks by using cotton related videos online,
STEM/Interdisciplinary lessons which are found in the cotton kit,
and Problem Based Learning through discussions of the eradication of
the Boll Weevil and issues of cotton farmers today that need
resolving-which could extend this task. It is through the
intersection of these three instructional tools – 3-Act Tasks,
STEM/Interdisciplinary lessons, and PBL - where students create
memorable, relevant experiences from real world scenarios that
students would not typically have access to. This is authentic
learning. Take a given task and bring it to life by creating a
hands-on experience for students. This will most likely require some
revision, and is enhanced with a real life problems or situations
for students to find possible solutions. Your students will thank
you for it. Keep Calm and Cotton On!



 The
Reflections staff would love to feature student artwork
upcoming issues of our journal. Do you know a budding artist? Have
you thought of collaborating with your school’s art department to
create something mathematically beautiful? Do your students create
mathematical artwork in your classroom? Please consider submitting
this work to Reflections! This would be a wonderful way to
highlight your school’s talent, creativity, and love of mathematics
within a public forum. In order to have Reflections showcase
your student’s work, please submit the following:
The
Reflections staff would love to feature student artwork
upcoming issues of our journal. Do you know a budding artist? Have
you thought of collaborating with your school’s art department to
create something mathematically beautiful? Do your students create
mathematical artwork in your classroom? Please consider submitting
this work to Reflections! This would be a wonderful way to
highlight your school’s talent, creativity, and love of mathematics
within a public forum. In order to have Reflections showcase
your student’s work, please submit the following:



 NCTM Vision: The National Council of Teachers of
Mathematics is the global leader and foremost authority in
mathematics education, ensuring that all students have access to the
highest quality mathematics teaching and learning. We envision a
world where everyone is enthused about mathematics, sees the value
and beauty of mathematics, and is empowered by the opportunities
mathematics affords. (Approved by the NCTM Board of Directors,
October 20, 2012)
NCTM Vision: The National Council of Teachers of
Mathematics is the global leader and foremost authority in
mathematics education, ensuring that all students have access to the
highest quality mathematics teaching and learning. We envision a
world where everyone is enthused about mathematics, sees the value
and beauty of mathematics, and is empowered by the opportunities
mathematics affords. (Approved by the NCTM Board of Directors,
October 20, 2012)