 |
Vol X No. 3 Fall |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Photo credit - Becky Gammill
By now, most of us are settling into a new school year. We have new classes, new faces (both children and adults), new challenges, and new expectations. Starting over every year, although stressful at times, should be viewed as a new adventure with endless possibilities. I am already feeling the excitement building as final preparations are being made for the Georgia Math Conference at Rock Eagle in a few short weeks. To kick off the conference, we have an exciting event happening on Wednesday afternoon. Therefore, plan to arrive by 3:00 p.m. on October 17th, if possible. There is a full slate of keynote and featured speakers and breakout sessions planned. However, the best part of coming to Rock Eagle is renewing old acquaintances, making new friends, and doing math! I look forward to seeing you there. This past summer, I attended a leadership conference in Denver. My husband was able to go with me, and we extended our trip to include a wonderful Colorado vacation. We did all the tourist "gigs." We went to Star Wars Night at a Rockies game and watched the sun set behind the Rocky Mountains in the outfield. We made it to the top of Pike's Peak, went whitewater rafting on the Colorado River, drove through Rocky Mountain National Park, saw snow in August, survived sleeping in the "Stephen King" room at the Stanley Hotel, and observed fascinating wildlife. It was a wonderful experience, and we filled our days with as many activities as possible. After we returned home, and I began my new year, I realized that I am not the same person I was before my trip. I felt different. I saw incredibly beautiful scenery and met so many new people- each one with a unique story. From the couple we met on the train who showed us downtown Denver to our river guide whose parents were educators that greatly impacted Special Education programs, I developed a deeper understanding of the world around me. At the conference, I worked with teachers from Singapore, Canada, many from the Denver area, and others from all over the country. As we exchanged ideas and talked about our experiences, all of us had more to take back with us. Having the opportunity to share experiences with math teachers, coaches, and administrators from all over the world has made me a better teacher and learner. By sharing some of the resources we use in Georgia, including the Georgia Numeracy Project, with teachers who are looking for ways to better serve their struggling students, I now have a richer appreciation of the importance of such valuable resources. As with our students, by explaining this Project to other educators, I have a better understanding of how it all fits together. As I complete my term as GCTM President at the end of October, I would like to leave you with some advice -- take advantage of every opportunity you have to grow as a person. As you attend a conference or training, as you try something new in your classroom or at your school, or as you visit new places, take time to prepare yourself to be affected. Approach each challenge with the mindset of "what have I learned from this?" Value any opportunity you have to collectively collaborate with others and reflect on the benefits of these conversations. I recently attended a presentation where the speaker discussed many innovative concepts. Initially, I felt that I didn't take away many new resources or ideas. The next day, I discussed the presentation with a colleague, who also attended this presentation. As we brought up some of the topics and how they impacted our way of thinking, we quickly realized that we got much more out of the evening than we originally thought. This is why it is so important for us to allow our students to collaborate as often as possible with each other in the classroom. The learning potential increases dramatically when the conversation involves more than just the teacher. As you prepare for the 2018 Georgia Math Conference, bring an open mind and expect to be changed. Embrace the opportunity to grow and learn. Teachers spend so much time giving to and providing for others; take this time to rejuvenate. Do this for yourself. My tenure as GCTM President afforded me many opportunities that I would not otherwise have been able to experience. Relationships, networking, and learning from others across the country and the world have helped me to continue to become a lifelong learner. Thank you for the privilege of serving as your GCTM President. During my travels, it has an honor to be a Georgia teacher who represented such an outstanding body of mathematics educators. Don't worry -- I am not going away. I will continue to be active within GCTM. I plan to continue to grow and develop as a teacher and a person while looking for ways in my everyday experiences to shape who I become. "Be patient with me ... God isn't finished with me, yet."
The conference provided the opportunity for attendees to participate in professional learning, network, and complete individual affiliate work. Dr. Jeffrey Wanko of Miami University in Oxford, Ohio led professional learning related to Supporting High Quality Teaching and Learning. After referring to the "Mathematics Teaching Practices" from Principles in Action, he engaged participants in a secondary mathematics task. Participants identified several effective teaching practices that were employed while being engaged in the rigorous task. Getting a glimpse at Chapter 7 "Key Questions to Guide Teachers in Supporting Productive Struggle in Learning Mathematics" from the 2017 NCTM publication Enhancing Classroom Practice with Research behind Principles to Action was especially interesting since "Embracing Productive Struggle" is the theme of the 2018 Georgia Math Conference. Affiliates shared bright spots that were of great interest to others. Other affiliates were interested in hearing about GCTM's Math Day at the Capitol and the Summer Academies. Individuals holding similar offices were given the opportunity to meet to share about ideas. The advocacy efforts of NCTM were shared by Dave Barnes, Associate Executive Director for Research, Learning, and Development. The GCTM delegation reviewed and supported the goal identified last year, "Teachers need to be equipped with additional strategies to provide all students access to rich, relevant, and rigorous learning experiences that address appropriate standards." Further work included discussing and suggesting wording to clarify GCTM Policies and Procedures. The Affiliate Leaders Conference not only provides the opportunity to get ideas from other affiliates and get suggestions on how to improve current initiatives, it allows affiliates to share successful and effective programs that may benefit other affiliates. It provides affiliates the opportunity to collaborate, another strategy to enhance practice.
Former MAA president Francis Su has, in my opinion, composed one of the most impactful and important statements concerning why we teach mathematics. The link below to Dr. Su's blog post includes the text of his retiring presidential address, at the January 2017 Joint Meeting of the MAA and the AMS in Atlanta, in which he makes us all think about why we teach mathematics. I was fortunate to be in the second row of the audience for this presentation. I am not ashamed to say that I cried at the conclusion of his presentation, not just for his eloquence and poignancy, but also because I realized that I fall far short of where I want to be as a teacher of mathematics. But Francis Su's words have given me renewed purpose as a teacher of mathematics: I can help people flourish. I have watched the video three times since, and read his blog post twice. I will most likely watch it or read it again -- particularly after I've had a rough day, when I need reminding of why I do what I do. If you choose to read the blog or watch the video, perhaps you will be moved like I was, or perhaps you will believe it was a waste of your time, but either way, you should ask yourself: why do you teach mathematics?
Governor's Race:
With all the national attention on the Governor's race, how does Democrat Stacey Abrams make it close? The math is actually very simple. Gov. Nathan Deal was re-elected in 2014 by roughly 200,000 votes over a well-funded candidate, Jason Carter (the former president's grandson.) A third-party candidate received 60,000 votes or 2.4 percent. There are two third-party candidates on the ballot in 2018. Abrams' challenge will be to grow the off-year electorate by roughly 250,000-300,000 if you assume she gets every vote Carter got in 2014.
Both candidates will bring in the luminaries and idols of their base, but the race will come down to these factors:
What will the record be and how much outside money will flow? This race has already set a record with over $30 million spent in pursuit of the nominations of both parties. Lt. Gov. Casey Cagle raised and spent more than $12 million in a losing effort.
Capitol Influence:
There are three important considerations as the transition of power in the state Capitol starts to play out:
We will continue to keep you informed during the coming months.
GCTM Outreach
GMC
--
The State Superintendent Candidates Forum:
Classroom Visits:
Math Day at the Capitol:
"The 2018 Summer Academies were fantastic. So many wonderful conversations occurred between so many teachers at each grade level! As one participant said, "This course was undeniably one of the best professional development courses I have ever attended. There was a plethora of information presented that I can utilize in my classroom. I am excited about the tools I've gained to build discourse."
This year the Academies were held in Coffee County, Pickens County and in Houston County. Over 300 math teachers came together for two days of collaboration and learning. The focus for this year was facilitating quality math discussion amongst students. The teachers learned strategies that they may use in their classroom to increase student knowledge while they are discussing math with other students. While planning for the Academies, the facilitators used the book 5 Practices for Orchestrating Productive Math Discussions. The teachers learned to set clear goals and anticipate student responses. Planning for how students might solve problems allows the teacher to think about what discussion needs to occur while the student is working. Monitoring student responses to a problem lets the teacher focus the mathematical discourse on the important concepts and to keep track of the students thinking. Selecting and sequencing the students' work to share with the class are crucial steps in facilitating and encouraging mathematical discussions. This careful selection of students to share their work allows the teacher to control what is discussed and when; focusing the conversation on the important concepts and/or clearing up misconceptions that the students may have. Teachers also learned how to craft questions and compare work so that the students can make connections between prior knowledge and the current knowledge being developed.
Engaging tasks and games to use with students was also a major focus. Since the sessions within the Math Academies are arranged by grade-band, the teachers are able to focus on tasks and games that can immediately be used in the classroom. The Academy participants learn to develop high-quality mathematical discourse within their classrooms while engaging in grade-level appropriate tasks. One participant stated, "I got a lot of very usable tasks that can be easily scaffolded for use in my regular education class as well as my Honors class."
Middle and high school teachers also learned how to code and how to incorporate coding into the math standards for the grade level. Teachers were so excited when they worked so diligently with a team to apply mathematical knowledge and code the robot. Teachers applied knowledge of geometry and measurement of angels to make the robot follow a path or create a shape. Watch these videos to see the awesomeness of these teachers and their coding skills!
During the Lunch-N-Learn sessions at each Academy, the participants learned about questioning techniques to help guide student thinking and learned to use Cuisenaire rods to create conceptual understanding. Lunch was provided for these lucky Academy participants and the extra knowledge helped propel them back into the classroom ready to meet the needs and demands of students.
Even after all of these fantastic ideas for teachers was shared and discovered, many participants felt that the time to collaborate with other teachers was the most valuable part of the Academy. New tasks are great and so are new strategies to use in the classroom, but creating a connection to a colleague that you can continuously learn from is invaluable. One participant said, "I really enjoyed working alongside other math teachers. I am the only math teacher on my grade level and it was really awesome to collaborate with others." We even had a visit from Georgia's House of Representative Robert L. Dickey, III. He spent about an hour visiting each session of the Academy and talking to the teachers of Georgia. Representative Dickey even learned how to use a calculator to write code for a robot. He was very supportive of the teachers and seemed impressed that so many teachers were giving up their summer in order to improve mathematical instruction for students.
I have traveled the state and participated in the GCTM Summer Mathematics Academies for many years and I am always blessed with new colleagues, new ideas, and new strategies that I can use to make a difference in the mathematical life of a student. To me, it is worth giving up a small part of my summer to change the life of a child. I hope each of you will join us for the 2019 GCTM Summer Mathematics Academies! Look for dates and places to be announced during the 2018 GCTM Math Conference at Rock Eagle!
For example, last spring I visited a trendy coffee shop while on vacation. As I waited for my coffee, I noticed some beautiful wooden platonic solids on a shelf. I stood in amazement at the mathematics I had stumbled upon and finally asked the shop owners, "Are these items for sale?" "Actually, no," she responded. "A regular customer gave those to us as a gift. He works in construction, but he makes these for fun. Would you like me to call him to see if he has any others for sale?" Of course I jumped at the opportunity to meet Tony, the artist and builder who designed the pieces. The following day, I met him and his beautiful wife for coffee and enjoyed a long, rich, and rewarding mathematical conversation.
He spoke of his mathematical hobby and how he constructed the polyhedra in his basement for fun. He even brought a few samples for me to take back to my classroom (for free!). Along with the platonic solids, he brought a unique three-dimensional model that he designed to help novice roof builders determine the roof-pitch measurements given certain criteria. He used the model to explain how trigonometric ratios, similar right triangles, and inverse trigonometric relationships were critical components to determining pitch. Tony was also surprised when I pointed out some applications of geometric means within this model. (I will write about this in greater detail for a later Reflections issue.) For three hours, we discussed our respective mathematical professions and expressed appreciation for finding another kindred spirit who understood our deep respect for both the beauty and usefulness of mathematics. And, in this case, the connection we made was indeed platonic (pun intended). These conversations can happen anywhere. You have to be open to finding them, and in some cases, willing to be a little bit vulnerable in meeting someone new. For instance, at a local Chick-fil-a fast food restaurant, I met an interesting man studying for his engineering certification exam. While my daughter was playing in the toddler area, I noticed him studying mathematics in a booth. Adam surrounded himself by course textbooks, calculators, and scratch paper riddled with mathematical work. He sat concentrating on his work with a calculator in his hand and his head resting in the other. I'm always intrigued by these scenarios. I tend to wonder what they are studying and whether I could help. At first, I assumed that this student was in a college class. As my daughter and I were leaving, I spied the normal curve and the Empirical Rule on the pages of his text. I thought, "Now I can help with statistics..." So I boldly asked, "I'm sorry to bother you, but I can't help myself...What are you studying?" He smiled and said, "I'm studying for the CPE." The CPE is a Certified Professional Engineer exam, and Adam was an alumnus of Southern Polytechnic Institute (now Kennesaw State University's Marietta Campus). He explained that he also had to take the Fundamentals of Engineering exam since he did not take it as a senior because he was already working as a principal engineer at the time. Now, even though he was already a professional thermo and fluid engineer, but he found himself studying and feeling like a student again. In the workplace, he debated with his colleagues about the mathematics behind his proposals, and as he explained to me, "Although I'm usually right, they would often say, 'Yes, but are you CPE certified?' to discredit me." This motivated Adam to pursue his CPE certification by taking "the hardest math test you can image." He described the CPE as a challenging, eight-hour, 1,200-question multiple-choice exam that covers a plethora of mathematical courses he had taken years ago. I, once again, found myself admiring the mathematical passion of a stranger. He loved his field, and he was using mathematics to earn more respect and credibility in that field. He wanted to not only pass the test but to beat it. That day, I found a valuable human resource in the form of a talented engineer who wanted to share his passion for engineering my students. The encounter humbled me because I first thought I could help him with his studies, but it was he who had knowledge of applied mathematics that far exceeded my own. During our brief conversation, we discussed the joy of challenging ourselves with mathematics, and how fortunate we were to find an engaging and satisfying career working with math on a daily basis. He also possessed a passion for engineering and was open to teaching teenagers how much fun and lucrative a STEM career could be. Mathematical encounters happen in a variety of contexts--the grocery store, the gym, social gatherings, or even at the dinner table. Mathematical discourse in real-world contexts solidifies why people pursue either personal or professional connections with mathematics. These precious conversations have informed my knowledge of how people in other contexts use mathematics and I've connected with more relatable human resources to introduce to my students. Users of mathematics outside the classroom can uniquely speak to skeptical students to explain, in a more "real" way than I can, how mathematics is relevant in vocational contexts while also inspiring these students through their genuine passion for the subject. This is why we should all seek out and try to connect with mathematical people in our everyday contexts. Ask bold questions and take the risk of learning something new. After a mathematical encounter, write down what you've learned and how it applies to your students or content area. When you carry these narratives, resources, or people back to your students, you will underscore how we live in a mathematical world surrounded by people who use mathematics every day. These connections humanize and authenticate mathematics, and your demonstrated boldness and vulnerability to engage in mathematical discourse will model how to be a lifelong learner of mathematics for your students.
Abstract The focus of this research project is to identify best practices in eighth-grade mathematics teaching and learning. Our methodology is to identify school systems who face high poverty, yet whose students reach high levels of achievement as indicated by the Georgia Milestone Assessment System (GMAS). Within the 29 Georgia counties with the highest poverty rates in the state, we identified four counties with the highest percentage of students performing proficient and above on the GMAS. Teacher survey results at the high-performing middle schools in these counties reveal the importance of continuous assessment, grouping strategies, high expectations, technology use, strong curriculum, and a variety of instructional methods. In addition, the surveys indicate that in order to meet the specific needs of students in poverty, schools need to: (1) address students' nutritional needs, (2) provide supplies to students, (3) seek out families in need and immediately provide help, (4) demonstrate to students that you care about them, (5) increase the curriculum at school in order to decrease homework expectations, and (6) obtain external technology grant. From 2003 to 2015, the state of Georgia has continuously closed the gap with the nation in 8th-grade math performance as measured by the National Assessment of Educational Progress (NAEP). During the past 2 years, this improvement has stalled. So, how can we start narrowing the performance gap again? One way of improving overall performance is to identify low performing groups of students and determine how to better reach them. Children living in poverty are more at risk of underperforming when compared to their counterparts not living in poverty. Research conducted by the NAEP showed nationally that only 18% of 8th grade math students who were eligible for the National School Lunch Program reached the level of at or above proficient, while the overall percentage of 8th grade math students in the nation who reached the level of at or above proficient was 32% (NAEP Report Cards). In Georgia, only 15% of 8th-grade math students eligible for the National School Lunch Program performed at the level of at or above proficient, while the overall percentage of 8th-grade math students in Georgia who reached the level of at or above proficient was 28% (NAEP Report Cards). Clearly, poverty is a major impediment to success in mathematics. Is it possible that the performance gap between Georgia and the nation could be narrowed again if more students in poverty began to perform at a proficient level? By identifying high performing schools in high-poverty areas, we can determine the reasons for this high performance, in order to better reach math students in Georgia who live in poverty. Methodology In the U.S. Quick Facts: Persons in Poverty, the U.S. Census Bureau divides the counties of Georgia into five categories based on the percentage of people living in poverty with the lowest percentage category of 5.7-14.9% and highest percentage category of 26.8-39.2%. There are 30 Georgia counties in the category with the highest level of poverty. According to the Quick Facts, Clarke County is a high poverty county. However, research indicates that poverty rates are over-reported in towns near a large university, as in Clarke County's case, University of Georgia. Therefore, we excluded Clarke County from our study (Benson & Bishaw). NAEP assessment data does not break down scores by county. Therefore, to identify which of the 29 counties have high-performing schools, we studied the Georgia Milestone Assessment System (GMAS) from the Georgia Department of Education, which publishes the results of the GMAS by county. In order to select the high-performing counties, we chose counties with at least 40% of students scoring at or above proficient on the GMAS. We chose this minimum value as it is significantly higher than the overall state's percentage of 34.5% (Georgia Department of Education). According to the 2016-2017 Georgia Milestones Statewide Scores Spring 2017 School Summaries, there are four counties of the 29 high-poverty counties which significantly exceeded the state of Georgia's percentage of students at or above proficient (Georgia Department of Education). See the table below.
Table 1- Georgia Milestone High-Performing Counties
The Georgia Department of Education also provides assessment data for all the schools within these high-performing counties. The Spring 2017 Georgia Milestones End-of-Grade Assessment for these schools is shown in Table 2.
Table 2- Georgia Milestone High-Performing Schools We emailed the survey below to the eleven 8th grade math teachers at these schools.
If we did not receive a response, we repeated the request two more times. After sending the survey request three times, five of the eleven teachers responded.
Results of the Surveys When asked about instructional methods or other aspects that the teachers deemed important to their students' success, we found that most of the teachers stressed the importance of assessments, grouping strategies, high expectations, and technology. Some also referenced their curriculum and actual instructional methods. The first main focus was assessments, mainly formative assessments. These formative assessments varied in timing at different locations in the lesson. For example, Mauri Jarrard, an 8th-grade math teacher at Telfair County Middle School, uses an informal or formal assessment prior to covering new content. This enables her to determine the student's background knowledge and fill in any missing skills. Sabrina Rentz, another 8th-grade math teacher at Telfair County Middle School, utilizes formative assessments during the lesson. Rentz stated, "Students have numerous opportunities to show what they know during the lesson by utilizing an array of assessments, such as stick-its, whiteboards, thumbs-up/down, agree/disagree, Socrative app, and Quizizz. These results are used to gauge my students' understanding of the content and adjust instruction." Eighth-grade math teacher, Siterro Wheeler, mentioned another opportunity to use formative assessment. After exposing her students to the new content one day, the next day Wheeler uses a formative assessment to determine daily grouping for students. This enables the students to practice the new ideas learned on the first day of the lesson. Another location of formative assessment use is at the end of the class. Not only does Jarrard begin the new content with an assessment, she also ends each day with one in order to assess the students' learning of the content introduced that day. Some of her practical examples are: ticket out the door, think-pair-share, writing assignment to explain their learning for the day, and demonstrating understanding of the content via a hands-on activity. Not only are teachers at the high-performing schools conducting formative assessments, they are also continuously assessing informally during the lesson. Wheeler is constantly rotating throughout the classroom. This allows her to be able to assist any student as needed while they complete their independent practice. She also repeats and asks questions about the topic throughout the lesson. Additionally, Wheeler has students summarize the main vocabulary terms and main concepts as a class. Likewise, Rentz informally assesses while students work in groups together. Informal assessment allows both of these teachers to determine what their students know or where they are lacking understanding so they can adjust as needed. Secondly, the teachers heavily utilize grouping strategies. The surveyed teachers use formatives assessment to group students. Rentz said, "All groups are created with a purpose. Sometimes I utilize heterogeneous groups to allow for peer tutors and at other times I use homogenous groups with leveled work that matches their abilities." This method allows the grouping to be fluid and benefit all students. Wheeler also describes her use of formative assessment for grouping as, "A formative assessment is given to the students to determine daily grouping. Based on the formative assessment, students either work independently on a rigorous assignment or they work in a small group led by me to strengthen their understanding of the concept." Thirdly, the teachers attributed their students' success to high expectations. Rentz stated, "It is my belief that another major impact on my students is the high expectations that I hold for them regardless of their ability levels. My classes are grouped based on ability and my lower achieving class is exposed to everything my other classes are. They are expected to be able to succeed with the same content as everyone else. I use the assessments to see what parts of it I need to differentiate, but I never decrease work amount as differentiation. The type of differentiation that I utilize has students learning the same material and practicing on the same material, but maybe in different ways. I require them to dig deeper into the content and expand on that. High expectations play a tremendous part in student success. They are going to perform to the expectations you have for them." A teacher, who asked to remain anonymous, echoed Rentz by saying, "Students must be held to a high standard. Expect every student to excel." Not only should individual teachers convey high expectations, the whole school should also hold each student to a high standard. Wheeler praised her school for conducting a major school-wide initiative that "raised the bar for all students." This included implementing PBIS school-wide and having teachers create lessons that are "rigorous and challenging while meeting the needs of every student." From reading the teacher responses, communicating clear and high expectations to the students is a major key to their success. The fourth major aspect of student success mentioned by many of the teachers is the use of technology. Technology is a way to keep students engaged. Additionally, technology is very mobile and versatile. Walker uses it for students to practice tests online through the academic software Study Island. Rentz and Jarrard stress the importance of giving every student access to some form of technology. "We expose our students to various forms of technology. Our students have access to Chromebooks, iPads, SmartBoards, and calculators. The SmartBoard is used almost daily to provide instruction and occasionally used for student activities. Each math teacher has a class set of iPads that can be used for assessment and activities", stated Jarrard. Likewise, Rentz expresses, "We use technology on a daily basis in the classroom to increase student success. The iPads are used for different performance tasks, review activities, and assessments. By incorporating technology, we are able to reach more of our students and keep them actively engaged." Fifth, the teachers stressed the importance of a strong curriculum. When discussing curriculum, every teacher varied in his or her response. Some use only the Georgia Performance Standards and supplement with various resources. One teacher mentions, "When looking for resources, the focus is to solidify the understanding of the content and to provide appropriate rigor." Similarly, another teacher revealed that she uses the Georgia Performance Standards and the Engage New York (ENY) curriculum. "I really like the ENY approach because it is more rigorous, and the methods are mathematically sound. The curriculum is based on the deep understanding of mathematical concepts rather than just procedures," she said. On the other hand, one uses Glencoe Math by McGraw-Hill as her main math curriculum. She states, "It helps me as a teacher to be better prepared to differentiate my instruction, which in turn will help the students achieve success." After reading all of these responses, there was another aspect that was intriguing. Bethune Middle School has created two math classes for the 8th graders. Walker states, "Our principal made a crucial decision in 2014-2015, he added a support math class to 8th grade during the first year of GMAS, so 8th graders had two math classes. In one class, students learn the standards through units. The support math class is used to reinforce concepts and do extra practice. In my opinion, the addition of the second math class has been the reason for our higher than the state's percentages in the proficient and exceeding levels of the mathematics GMAS. I really believe the reinforcement during the 2nd math class in addition to the extra hour of practice has made the biggest difference in the scores." Lastly, the teachers reported using a variety of instructional methods to meet the needs of their students, such as:
Addressing the Needs of Students Living In Poverty In order to address the needs of students living in poverty, the high-performing schools, oftentimes in collaboration with their school systems, seek and utilize external partners and consider the special needs of students living in poverty. In particular, the respondents credit the following for impacting student learning and success at their schools:
Conclusion By studying schools in high-poverty areas that have achieved high levels of student success, we have found the following key components of success: continuous assessment, grouping strategies, high expectations, technology use, strong curriculum, and a variety of teaching methods. We believe that all students at all schools in Georgia will benefit from these components of success. Further, all schools have at least some students who live in poverty. In order to address their specific needs, our study found that schools and school systems need to: (1) address students' nutritional needs, (2) provide supplies to students, (3) seek out families in need and immediately provide help, (4) demonstrate to students that you care about them, (5) increase the curriculum at school in order to decrease homework expectations, and (6) obtain external technology grant. Acknowledgments: We wish to thank the 8th-grade math teachers Mauri Jarrard and Sabrina Rentz at Telfair County Middle School, Suraya Walker at Bethune Middle School, Siterro Wheeler, and an anonymous teacher for both their dedication to their students as well as their willingness to take the time to provide well-thought-out responses to our survey. We also thank the principals Danny McCoy at Bethune Middle School, Christopher Ellis at Telfair County Middle School, and Elaine Merritt for connecting us with these excellent teachers. References Benson, C., & Bishaw, A. (2017, December 07). Examining the Effect of Off-Campus College Students on Poverty Rates. Retrieved April 09, 2018, from https://www.census.gov/data/tables/2017/demo/income-poverty/acs5yrs.html Georgia Department of Education. (2017, July 20). Georgia Milestones 2016-2017 Statewide Scores. Retrieved February 19, 2018, from http://www.gadoe.org/Curriculum-Instruction-and-Assessment/Assessment/Pages/Georgia-Milestones-2016-2017-Statewide-Scores.aspx The Nation's Report Card. (n.d.). NAEP Mathematics. Retrieved February 10, 2018, from https://www.nationsreportcard.gov/math_2017/#states/scores?grade=8 United States Census Bureau. (n.d.). U.S. Census Bureau QuickFacts: United States. Retrieved March 01, 2018, from https://www.census.gov/quickfacts/fact/map/US/IPE120216#viewtop
A new school year always brings with it the excitement of a new group of students and renewed energy to plan and teach engaging lessons that not only meet the standards but also prepare students for their life after high school. Teaching the traditional "Three R's", Reading, Writing, and Arithmetic, leaves students lacking the skills they need for the 21st century. In addition to subject matter knowledge, today's students must be skilled in critical thinking, communication, collaboration, and creativity (the "Four Cs") (National Education Association, 2010). Educators must complement their subject matter content with the "Four Cs" to prepare young people for citizenship and the global workforce (National Education Association, 2010). The "Four Cs" can be incorporated into any classroom, but it requires educators to be intentional and purposeful in their planning. If students are going to be equipped with 21st-century skills when they graduate high school, they must have been provided opportunities to develop these skills throughout their schooling. Unfortunately, there is not a single resource that educators can implement in their classroom that will address all of the 21st century needs of their students. The flood of technology resources provided for educators is vast. Sorting through the plethora of resources in order to find the perfect combination that will address all of the "Four Cs" in one lesson will most likely leave the educator feeling defeated and overwhelmed. However, the skills students need for the 21st century, critical thinking, communication, collaboration, and creativity, can be addressed by taking advantage of technology, utilizing group activities, assigning project- and problem-based learning, and most importantly, sharing resources.
Time constraints often impede the ability to incorporate opportunities to strengthen students' creativity. However, in the math classroom, creativity can easily be integrated into the class by creating an environment where students are encouraged to develop innovative ways of solving a problem and are praised for sharing their original solution. Math educators should incorporate problems into their classroom that can be solved using multiple methods or have multiple solutions. This encourages students to use a wide range of skills and think outside of the box. Students should have access to materials inside the classroom so that they can creatively problem solve. Additionally, students should be encouraged to use a variety of technology resources, such as building a website through Google sites, creating a movie using an iMovie, or comic strip through canva.com. Integrating the "Four Cs" into the mathematics classroom does take some research and planning, but these efforts will benefit students as they prepare to enter the current workforce. Educators should not feel overwhelmed by attempting to address all of the "Four Cs" in one lesson. Instead, educators should focus on one or two of the "Four Cs" and slowly integrate new technology resources into their classroom. Incorporating technology resources, group activities, project-based, and problem-based learning in the mathematics classroom will help to develop the skills students need to be successful in the 21st century. References National Education Association (2010). Preparing 21st Century Students for a Global Society: An Educator's Guide to 'The Four Cs'. [online] Washington DC: National Education Association. Available at: http://www.nea.org/assets/docs/A-Guide-to-Four-Cs.pdf [Accessed 24 Jul. 2018].
Implementing open tasks that reveal students' misconceptions can be unnerving for any teacher, and supporting students' discourse about those misconceptions can be equally challenging. Such tasks and discourse can be especially difficult with younger students who are still developing communication skills, but engaging in their use can be rewarding for students and teachers. In this paper, we describe the design of, enactment of, and reflection on a lesson in which technology was used to revisit ideas from a previous lesson, to support first and second-grade students in arguing and confronting valid and invalid strategies for measuring length in order to develop deeper understandings of aspects of measurement.
We describe the lesson in more detail below, but first, give an overview of its affordances and limitations. This lesson, collaboratively developed by a mentor teacher, an intern teacher, and a teacher educator (first author), was productive: students tried out strategies, discussed their ideas, were surprised when they saw strategies that resulted in different answers, and argued about why the answers were different and why they were not correct. At the same time, the lesson was messy: we knew not all students left the lesson with a perfect understanding of length measurement, and it was difficult to measure new growth or new understandings for each student. The teachers and the first author reflected on the lesson and considered potential improvements. We all felt confident that the benefits from the discussions, arguments, and confrontations of misconceptions had at least added to the students' foundations for later understandings.
We describe the development, enactment, and reflection on this lesson in this paper, with one focus on acknowledging and accepting that the mathematics and learning outcomes that emerge from this approach can be messy and difficult to measure, but are also valuable. A second focus is on the complexity of interaction between pedagogy, mathematics, and technology. That is, the pedagogy involved implementing an open, multi-level task and facilitating productive discussion at points in the task, the mathematics involved attention to sophisticated aspects of length measurement such as unit-attribute relations, partitioning, and tiling (explained below), and the technology was used to build on a previous, concrete task and to focus student attention on particular strategies.
Background and Method
Ms. Holst, an intern teacher in a full year teaching field experience, worked with a mentor teacher who had taught for ten years. The elementary school was a Title 1 school with students at a wide range of mathematics proficiency levels based on standardized mathematics testing. The classroom in this paper combined 28 first- and second-grade students (14 at each level). Following recommendations from Mathematics Teaching Practices from Principles to Actions: Ensuring Mathematical Success for All (National Council of Teachers of Mathematics, 2014), Ms. Holst's mentor teacher incorporated challenging tasks and student discourse into mathematics lessons. She valued developing classroom norms encouraging students to make and test conjectures, make claims, and support claims with evidence to support their development of conceptual understanding and procedural fluency. She supported students' metacognition by asking them to reflect on their thinking and to notice when it changed. She also asked her students to engage in challenging tasks. After a task, she frequently asked students to reflect on their strategies by viewing examples of work done by unknown (imaginary) students that illustrated different ways of thinking and misconceptions. The mentor teacher asked students to explain what they thought the imaginary student was thinking and then to revise their initial solutions based on their new thinking.
In collaboration with her mentor teacher, Ms. Holst designed and taught a lesson focusing on length measurement to her combined first- and second-grade students. The lesson incorporated van de Walle et al.'s (2013) Crooked Path activity (see Figure 1). Ms. Holst created crooked paths similar to those in Figure 1 using masking tape on the floor and on some tables. Students worked individually. They used physical objects to measure paths, recorded their measurements, and moved to the next path. Ms. Holst felt her lesson engaged her students in experimenting with length measurement. However, because of the classroom management and logistics involved in facilitating students' movement from path to path, and because students were measuring and recording individually, Ms. Holst felt she missed important aspects of student thinking and insight in the end-of-lesson discussion.
Figure 1. Examples of "Crooked Paths" (Van de Walle, 2013).
Planning the Lesson
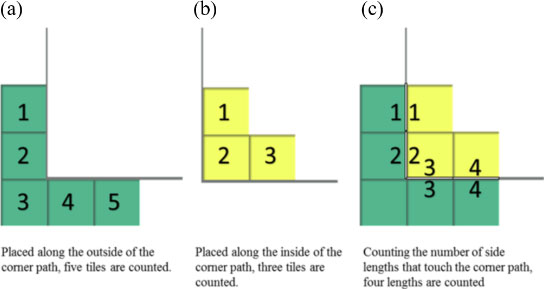
Ms. Holst and the first author planned a follow-up length measurement lesson for the initial physical object implementation of the Crooked Paths task. Ms. Holst's goals for the follow-up lesson were for students to build on the Crooked Paths experience by allowing them to (a) engage in a task designed to reveal misconceptions, (b) use a dynamic applet to view and then reflect on two common strategies, each revealing a different misconception, and (c) use the dynamic applet as a tool to support mathematical discourse about the meaning of units in measurement. As part of the planning, the author adapted the task based on discussions with Ms. Holst, creating a set of three applets to be incorporated into the lesson. We designed the lesson to support and elicit student thinking about unit-attribute relations, partitioning, and tiling based on Barrett & Clements' (2003) and Lehrer's (2003) discussion of these components for learning length measurement. Unit-attribute relations refers to students' ability to recognize the relationship between the unit that is used to measure and the attribute being measured. In the digital Crooked Paths task, unit-attribute relations emerged as students used a two-dimensional shape (e.g., a tile) to measure the one-dimensional attribute (e.g., length) of a path. Common misconceptions about the relationship between the tiles and the length of a path are allowed to emerge when corners are part of the path (see Figure 2). Students may place tiles around the outside of the corner, counting one extra unit because a tile fits outside the corner (see a). Students might place tiles around the inside of the corner, counting a tile in the corner once despite the two unit lengths (see b). Attending to the unit-attribute relationship, a student would skip the corner (green) or double-count the corner (yellow) to count 4 unit lengths (see c).
Figure 2. Counting tiles (2D object) compared to counting lengths (1D part of a 2D object).
Partitioning refers to the idea that the length must be divided into some number of equivalent spaces. That is, the lengths along a path identified by placing tiles must be the same size. When using concrete objects to measure length, partitioning means attending to precision to create unit lengths that are the same size; that is, avoiding gaps and overlaps (see Figure 3). The other side of partitioning, tiling, refers to the concept of filling the space completely (e.g., no gaps). This applet deliberately allows gaps and overlaps to allow misconceptions to be revealed and to allow students the opportunity to actively work on precision (when they notice the gaps and overlaps as problematic). The task supports students in developing their conceptual understanding of partitioning and tiling by allowing them to leave spaces or overlaps and then to confront the mathematical consequences when they compare solutions.
Figure 3. Mathematical consequences of gaps and overlaps include the possibility of infinite, distinct measures of the same length.
Lesson Plan
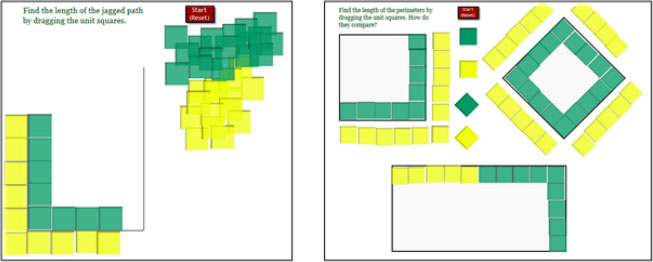
The lesson structure used a Launch-Explore-Connect-Explore-Connect format. Ms. Holst introduced the task by showing students how to open the applet and move the pieces. In teams of three or four, students found lengths for paths in Activities 1 and 3 (see Figure 4).
Figure 4. Activities 1 and 3 are shown on the left and right, respectively.
Ms. Holst led the class to compare solutions. They found groups had different solutions. She showed the students the video of Yellow over-counting and Green under-counting (see Figure 5). Ms. Holst asked students to discuss Yellow's thinking and Green's thinking in their small groups. She asked them to revise their strategies as needed. Finally, Ms. Holst led a whole class discussion where students shared their thinking and guided her through the tiling process to discover the misconceptions about Yellow's and Green's thinking.
Figure 5. Jagged Paths animation showing two common (but incorrect) strategies: underestimating and overestimating.
The lesson was the last of the day and took one hour. As students worked on their exploration of Activities 1 and 3, Ms. Holst asked groups to take screenshots of anything they thought was interesting. Of the nine groups, six groups took screenshots within a few minutes of each other. All screenshots are shown in Figure 6, in no particular order. The screenshots show different strategies used by students: placing tiles along the inside of the path, placing tiles along the outside of the path (with corner blocks and without corner blocks), and placing tiles that were centered on the path.
Figure 6. Screen shot images taken by six of the nine groups. (Some images are smaller or larger depending on student actions, but otherwise differences in size have no significance.)
Groups A, C, D, and F placed blocks along the inside of the path, while group B placed blocks along the outside and omitted the corners, and group E placed blocks centered on the line. Students' attention to placement without gaps or overlaps can be seen. Student groups shared the answers they had found, with most answering 15 tiles, one group answering 17, and one group answering 19 1/2.
Ms. Holst showed the green squares placement (Green's strategy) animation in Activity 2 (shown in Figure 7a), which results in the placement of 19 squares. She asked them, "What was Green's answer? What did the Green student do? Write about it!" After a few minutes of writing, she showed the yellow squares placement (Yellow's strategy) animation in Activity 2 (shown in Figure 7b), which results in 15 squares. Students acted surprised and several hands shot in the air, impatient to share. After a few minutes of writing, Ms. Holst asked students to discuss their reactions in their groups.
Figure 7. Screenshots from Activity 2. (a) Image shows Green's (wrong) placement and (b) Image shows Yellow's (wrong) placement of squares in contrast to Green's.
Students described their thinking in different ways showing a range of various understandings and various levels of ability in communicating their own thinking. A student in one group pointed to Green's corner squares and said, "Corners -- they put one in the corners." Another student answered, "The line on the inside is shorter. The one on the outside is longer." I asked him if the line was different lengths on different sides and he agreed, pointing to Yellow's path and Green's path. A student (Student B in Table 2) in a different group pointed to Green's path and said, "That's what we did. That's why we got 19. But the yellow is right. I have proof -- because more [groups] got 15."
After some time spent in group discussion, Ms. Holst called for students' attention. She asked them to share thoughts about Green's and Yellow's strategies. One student referenced the previous lesson in which students measured with objects. In that lesson, because the students kept counting with the first counted object as "zero," Ms. Holst explained to them that zero means "a nothing unit." Ms. Holst showed me that she had indicated the nothing unit by squishing her fingers tightly together. In explaining why the squares placed outside the corners of the path (and thus touching only a tiny bit), the student referenced that discussion by also pushing her fingers together while talking about the space at the corner being counted as zero. Ms. Holst did not feel satisfied with the students' explanations, because they had seemed to accept the inside (yellow) strategy. At the moment, she made a decision to continue the class discussion by asking students to be "Line Detectives." She opened Activity 1, using a computer behind the class. She wanted to support students in noticing that measuring the path was not counting the squares; rather, measuring the path was counting the number of side lengths.
First, she focused students' attention on the side lengths by asking them, "What is the unit we are using to measure?" Students responded with multiple responses, including "Inch" and "Kind of an inch like we used to measure things." Ms. Holst asked again, "Read the instructions again: 'Find the length of the jagged path by dragging the unit squares.' Hmmm. '...dragging the unit squares...' Maybe the unit isn't an inch. We just have a line that we're measuring -- is the unit square the unit?" One student answered, "On the side." Another student agreed, "She said, and I agree with her, to measure on the side." Ms. Holst responded, "Is the unit the whole square or the side? [moves a square] When am I measuring part of the line? You will be line detectives as I move the squares..."
Next, Ms. Holst placed the green and yellow squares, following the same paths as the animation. She asked students to carefully watch and tell her when a square touched the jagged path once, twice, or not at all. Students watched closely as Ms. Holst moved each square, placing it on the outside of the path. Frequently, a chant of "Gap!-Gap!-Gap!-Gap!-Gap!" went up. Finally, Ms. Holst stopped and said, "You guys are so good at noticing the gaps. But I'm doing the best I can with this mouse so just look for whether I'm measuring part of the line or not." When Ms. Holst reached a corner and placed a square at the corner, students yelled, "No!" When she finished placing the squares, the students counted with her to reach 17 squares touching the line. She repeated the process with the inside of the square, asking them "For the inside, is each square only measuring one unit of the line?" As she placed a square in the corner, she asked, "Is this square only measuring one unit of the line?" Some students said, "Yes" and others said, "No." Ms. Holst explained, "Actually, the square is measuring two units here -- so we need to count it twice." She and the students counted how many times each square touched the line. They counted twice at the corners to reach an answer of 17. A girl said, "What!"
Ms. Holst instructed them, "Write on the paper. What is your answer and how can you prove it's right?" Some students had already written an answer. One student asked, "Do you want our thinking now or from before?" Ms. Holst responded, "What is your answer right now and how can you prove it's right?" As I watched students writing, I asked some students to explain their answers to me. One student told me the answer was 17 and that he could prove it because it was how many times each square touched the line. His written answer only indicated that the answer was 17 because we had counted it twice for Green and for Yellow.
Lesson Outcomes
The enactment of the lesson had mixed results. Ms. Holst pointed out that one benefit of the lesson was providing students with the opportunity to show off the new thinking acquired from other measurement lessons, such as their thinking about the value of precision, avoiding gaps and overlaps, and applying the "zero unit." This attention can be seen in the groups' screenshots shown in Figure 4, where squares are relatively aligned and fitted closely together. One student even showed this value by remarking, "He's so good! He's being very precise!" Students also showed their attention to avoidance of gaps and overlaps during the last class discussion when they chanted "Gap!-Gap!-Gap!" as soon as they saw any space between squares. Another benefit of the lesson was exposing misconceptions of some students, especially with respect to gaps and overlaps and not connecting the act of measurement with the characteristic of the line that was being measured. These misconceptions are discussed in the next section.
Conclusion
Complex mathematical ideas cannot be learned in one lesson, but over time through messy work that allows student misconceptions to be revealed, and through discourse that allows students to confront their own misconceptions, show their newly acquired knowledge, and change their thinking. Building a measurement lesson that supports students' meaningful engagement in making sense of measurement ideas, arguing, thinking critically, and changing their own thinking is important to developing this knowledge but may problematize the measurement of students' gains. As Ball, Lubienski, and Mewborn (2001) wrote, "With focused, bounded tasks, students get the right answers, and everyone can think that they are successful. The fact that these bounded tasks sometimes results in sixth graders who think that you measure water with rulers may, unfortunately, go unnoticed" (p. 436). A lesson that ends even though not all students have reached the learning goal is not a failed lesson. Understanding measurement takes time, repeated opportunities, and opportunities to engage with mathematics in meaningful ways.
References
Ball, D. L., Lubienski, S., & Mewborn, D.(2001). Research on teaching mathematics: The unsolved problem of teachers' mathematical knowledge. In V. Richardson (Ed.), Handbook of research on teaching (pp. 433-456). New York, NY: Macmillan.
Barrett, J. E., & Clements, D. H. (2003). Quantifying Path Length: Fourth-Grade Children's Developing Abstractions for Linear Measurement. Cognition and Instruction, 21(4), 475-520. doi:10.1207/s1532690xci2104_4
Lehrer, R. (2003). Developing understanding of measurement. A Research Companion to Principles and Standards for School Mathematics, 179-192.
National Council of Teachers of Mathematics (NCTM). 2014. Principles to Actions: Ensuring Mathematical Success for All. Reston, VA: NCTM.
Van de Walle, J. A. (2013). Elementary and middle school mathematics: teaching developmentally (8th ed.). Boston: Pearson.
Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2013). Elementary and middle school mathematics: Teaching developmentally (8th ed.). Upper Saddle River, NJ: Pearson.
The 59th annual Georgia Mathematics
Conference The 2018 Georgia Math Conference at Rock Eagle, will be held Wednesday October 17 - Friday, October 19, 2018. We hope you will join us! This year promises to be a great conference! The theme this year is "Embracing Productive Struggle". Early registration opened August 1st. Don't miss out -- register for this conference today! As an added bonus, conference attendees will receive a voucher to get 20% off an NCTM book order during the subsequent week of the conference. GMC 2018 Keynote Speakers
FEATURED SPEAKERS Thursday, 10/18/18, 9:30-10:45 Kristopher Childs: "Every Child Has Genius Level Potential -- Are You Giving Them Time to Showcase It?" (K-5) Participants will engage in the 6 Stages of Effective Mathematics Instruction. Participants will make sense of a lesson design process, develop an understanding of rich problem-solving task selection and implementation, and explore an effective instructional model. There will be a keen focus on the impact of productive struggle during the problem-solving process. Thursday, 10/18/18, 1:45-3:00 Michelle Bateman: Math Rx for a Productive Struggle -- "Do the Math" (Grades 6-12) Do you often hear students saying, "I don't get this!" or "How do we do this?" Do you wonder about ways to help your students through the struggle they have in mathematics? Well, the best medication for the symptoms associated with Productive Struggle will be addressed in this engaging and hands-on math session. Through active participation, you will leave with a better understanding of how to develop lessons that support a Productive Struggle in a positive way using the "Do the Math" Protocol. Thursday, 10/18/18, 1:45-3:00 Kristopher Childs: "Using Data to Make Sense of Students Struggles" (K-12) Participants will learn how to develop an effective data-informed environment that is student-centered. Participants will explore effectively assessing student learning, providing meaningful feedback, and using data to inform instructional decisions. In real-time participants will engage with an assessment system and develop a plan of action to implement the assessment system. Friday, 10/19/18, 9:45-11:15 James Tanton: "The Power of Visualization in Mathematics" (K-12) This session will demonstrate the astounding power -- and fun! - of visual thinking in mathematics. Let's see just how fundamental and crucial pictures are to problem-solving, doing joyful mathematics and engaging in deep learning. Friday, 10/19/18, 9:45-11:15 a.m.: Michelle Mikes hosts a panel discussion, Mathematics Leadership in Education and Instruction: Promoting Productive Struggle (K-12, College)
We are all stakeholders in the education of our students. From the classroom teacher to legislators, how are you promoting mathematical productive struggle in and beyond your class? Join our panel of experts to learn how to pave the way for productive struggle opportunities with our stakeholders at large. Walk away with strategies in promoting productive struggle for success of student learning. Friday, 10/19/18, 1:00-2:00 Michelle Bateman: I See, I Hear, I Wonder -- Using Visual Literacy to Ignite a Productive Struggle (Grades 6-12) How do we get our students to persevere and make sense of the mathematics when they cannot relate at all to the mathematics being taught? Let's look at how Visual Literacy can be used to foster mathematical understanding and reasoning through thoughtful Math Talk and authentic work products. Through various simulations, participants will leave with tangible activities that can be incorporated in the mathematics classroom to ignite a Productive Struggle. SPECIAL CONFERENCE EVENT Escape Rooms will be available for educators of grades K-2, 3-5, 6-8, and 9-12 on Wednesday, 10/17/18, as a special pre-conference activity from 3:00-5:00 p.m.
State Superintendent Forum On Thursday, October 18th, GCTM will host state superintendent candidates Richard Woods and Otha Thornton for a live Q&A session. This forum will take place from 11:00-12:00 at Talmadge Auditorium at the Rock Eagle 4-H Center. Click here if you plan to attend and/or if you would like to submit one or more questions for the candidates to address during the forum.
Interested in becoming a GMC vendor? Please contact Jennifer Peek, Director of Exhibits at jennifer.peek@gctm.org.
During GMC, don't forget to check out some of the top-selling educational materials from NCTM! On October 18, sample publications will be on display in the vendor hall at GMC. This will give you a chance to preview items you may be interested in ordering. If you are a NCTM member, you receive discounts on the NCTM website for purchase. You will also get 20% off your purchase just for attending the conference. We look forward to seeing you there! Have you joined NCTM yet? Your membership comes with several perks. You receive:
Make sure that when you join, you click on the GCTM affiliate association which will give GCTM $3 - $5 for every membership. To sign up, please go to https://www.nctm.org/Membership
Your Membership Matters to GCTM
What can GCTM do to make your continuing membership a valuable part of your professional life? $20 is not a monumental cost for a year of opportunities to enrich your professional life and the mathematics education of your students. We want to offer you the opportunities and enrichment you most desire and find most valuable -- those that will keep you coming back year after year for more.
So let us hear from you! Take a few minutes to reflect.
What new ideas do you have that GCTM can put into action? Are you willing to volunteer? What can we do differently? Are you willing to invite a colleague to join? Brainstorm for ideas that will make us better, and then share them with us! Join the team as an active volunteer! Just contact us at any time at membership@gctm.org or go to gctm.org and contact any officer. You are GCTM! And we need all of you to continue this great legacy of the last 59 years!
|
Table of Contents President's Message - by Bonnie Angel, GCTM President NCTM Affiliate Leaders Conference (Summer 2018) - by Denise Huddlestun, President Elect and Chuck Garner, VP for Competitions 2018 Elections Update and GCTM Outreach - by T.J. Kaplan, Advocacy and Brian Lack Summer Heat, Summer Knowledge, Summer Time! by Kristi Caissie, Summer Academies Coordinator Mathematical Encounters - by Becky Gammill, Ed.D., Publication Editor Learning from High-Performing Middle Schools in High-Poverty Areas - by Gregory Harrell, Professor of Mathematics, Department of Mathematics, Valdosta State University and Anna Joy Holton, Senior Middle Grades Education Major, Valdosta State University Four Cs and Mathematics - by Dr. Julie Carter and Dr. Rhonda Amerson; both assistant professors within the Department of Teacher Education and Social Work at Middle Georgia State University Messy Lessons: Using Technology and Productive Discussion for Length Measurement - by Dr. Eryn M. Stehr and Dr. Ha Nguyen, both assistant professors of Mathematics Education at Georgia Southern University Georgia Mathematics Conference Information - by Martha Eaves, 2018 Program Committee Chair NCTM Report - by Michelle Mikes GCTM Membership Report - by Susan Craig, Membership Director
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Georgia Council of Teachers of Mathematics | PO Box 683905, Marietta, GA 30068 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 The
2018 Affiliate Leaders Conference was held in Indianapolis, Indiana
on July 9-11. GCTM was one of twenty-nine affiliate groups at the
conference and was represented by President Bonnie Angel,
Vice-President for Competitions Chuck Garner, and President-Elect
Denise Huddlestun. The theme of the conference was Supporting
High-Quality Teaching and Learning. NCTM President Robert Berry,
III, welcomed the group and gave updates during his presentation on
Advocating for High-Quality Teaching and Learning. He spoke
to the re-framing of Access and Equity "to include Empowerment, to
capture the critical constructs of identity, agency, and social
justice." He called on participants to advocate for: 1) "mathematics
coaches/specialists for ongoing real-time professional development
and support", and; 2) "teachers and mathematics coaches/specialists
to have time and space to collaborate with one another on
instructional issues and to continue their own professional learning
of both mathematics and mathematics-specific pedagogy."
The
2018 Affiliate Leaders Conference was held in Indianapolis, Indiana
on July 9-11. GCTM was one of twenty-nine affiliate groups at the
conference and was represented by President Bonnie Angel,
Vice-President for Competitions Chuck Garner, and President-Elect
Denise Huddlestun. The theme of the conference was Supporting
High-Quality Teaching and Learning. NCTM President Robert Berry,
III, welcomed the group and gave updates during his presentation on
Advocating for High-Quality Teaching and Learning. He spoke
to the re-framing of Access and Equity "to include Empowerment, to
capture the critical constructs of identity, agency, and social
justice." He called on participants to advocate for: 1) "mathematics
coaches/specialists for ongoing real-time professional development
and support", and; 2) "teachers and mathematics coaches/specialists
to have time and space to collaborate with one another on
instructional issues and to continue their own professional learning
of both mathematics and mathematics-specific pedagogy."












 You
are not alone. My students also ask, "When are we ever going to use
this?" Sometimes I give the playful response, "You know, this would
be a very nice pick-up line when meeting someone new. Picture it:
You catch someone's eye at a coffee shop and pay for his or her
mocha latte. As the conversation turns to the elegance of conic
sections, he or she will be so impressed by your mathematical
knowledge that he or she will ask you out! It happens all the time!"
While this particular scenario may seem implausible, I do believe
that a shared appreciation of mathematics is a wonderful conduit for
connecting with others.
You
are not alone. My students also ask, "When are we ever going to use
this?" Sometimes I give the playful response, "You know, this would
be a very nice pick-up line when meeting someone new. Picture it:
You catch someone's eye at a coffee shop and pay for his or her
mocha latte. As the conversation turns to the elegance of conic
sections, he or she will be so impressed by your mathematical
knowledge that he or she will ask you out! It happens all the time!"
While this particular scenario may seem implausible, I do believe
that a shared appreciation of mathematics is a wonderful conduit for
connecting with others. 





 Opportunities
to think critically and problem solve are essential in the
mathematics classroom. These learning experiences push students
from "doing" mathematics to "understanding" mathematics.
Problem-based learning and project-based learning are great ways
for math educators to increase critical thinking in their
classroom. These learning opportunities should incorporate
inductive and deductive reasoning, require students to interpret
information and draw conclusions, and solve unfamiliar problems
in both conventional and innovative ways. Robert Kaplinsky's
website (
Opportunities
to think critically and problem solve are essential in the
mathematics classroom. These learning experiences push students
from "doing" mathematics to "understanding" mathematics.
Problem-based learning and project-based learning are great ways
for math educators to increase critical thinking in their
classroom. These learning opportunities should incorporate
inductive and deductive reasoning, require students to interpret
information and draw conclusions, and solve unfamiliar problems
in both conventional and innovative ways. Robert Kaplinsky's
website ( Communication
represents a variety of interactions in the classroom.
"Expressing thoughts clearly, crisply articulating opinions,
communicating coherent instructions, motivating others through
powerful speech--these skills have always been valued in the
workplace and in public life. But in the 21st century, these
skills have been transformed and are even more important today"
(National Education Association, 2010, p. 13). While important,
face-to-face communication is no longer the primary way students
interact with each other.
Communication
represents a variety of interactions in the classroom.
"Expressing thoughts clearly, crisply articulating opinions,
communicating coherent instructions, motivating others through
powerful speech--these skills have always been valued in the
workplace and in public life. But in the 21st century, these
skills have been transformed and are even more important today"
(National Education Association, 2010, p. 13). While important,
face-to-face communication is no longer the primary way students
interact with each other.
 They
must continue to be taught how to communicate with someone
face-to-face, but must also be equipped with the skills to
communicate virtually and with people from different
backgrounds. In a mathematics classroom, students should be
communicating with the educator and other classmates through
multiple platforms. These could include email, Google classroom,
class website, making individual and group presentations inside
and outside of the classroom, creating a blog, and discussing
assignments with students in another state or country, to name a
few. The G Suite for Education by Google provides numerous ways
for students to communicate in and outside of the classroom.
They
must continue to be taught how to communicate with someone
face-to-face, but must also be equipped with the skills to
communicate virtually and with people from different
backgrounds. In a mathematics classroom, students should be
communicating with the educator and other classmates through
multiple platforms. These could include email, Google classroom,
class website, making individual and group presentations inside
and outside of the classroom, creating a blog, and discussing
assignments with students in another state or country, to name a
few. The G Suite for Education by Google provides numerous ways
for students to communicate in and outside of the classroom.
 Addressing
the "Four Cs" individually can be difficult. Through many of the
communication examples listed above, students are engaging in
collaboration. In a mathematics classroom, students must be
required to work in diverse teams to develop a solution to a
real-world problem. Fifty years ago, many jobs could be
completed individually. However today, much work is accomplished
in teams, and in many cases, global teams (National Education
Association, 2010). Through the use of resources similar to
Google docs and Padlet, students can collaborate with classmates
or students across the world. These learning experiences provide
students with the opportunity to strengthen their collaboration
skills.
Addressing
the "Four Cs" individually can be difficult. Through many of the
communication examples listed above, students are engaging in
collaboration. In a mathematics classroom, students must be
required to work in diverse teams to develop a solution to a
real-world problem. Fifty years ago, many jobs could be
completed individually. However today, much work is accomplished
in teams, and in many cases, global teams (National Education
Association, 2010). Through the use of resources similar to
Google docs and Padlet, students can collaborate with classmates
or students across the world. These learning experiences provide
students with the opportunity to strengthen their collaboration
skills.

















 GCTM
membership currently stands at 1142 members. This will increase a
small amount as conference registration continues.
GCTM
membership currently stands at 1142 members. This will increase a
small amount as conference registration continues. 
 What
are the best things GCTM has to offer?
What
are the best things GCTM has to offer?